Question

A variable circle is described to pass through the point (1,0) and tangent to the curve y = x. The locus of the centre of the circle is a parabola whose -

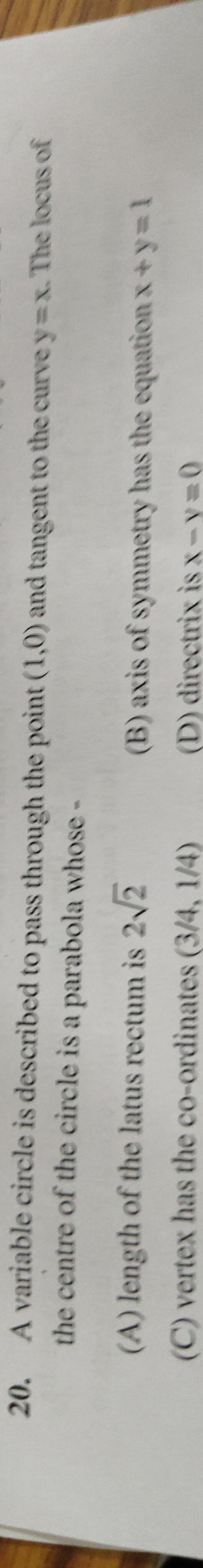
• A. length of the latus rectum is $2\sqrt{2}$
• B. axis of symmetry has the equation x + y = 1
• C. vertex has the co-ordinates (3/4, 1/4)
• D. directrix is x-y=0

Answer 1

Answer: (B), (C), (D)

(B), (C), (D)

Answer 2

The equation of a circle with center $(h, k)$ and radius $r$ is $(x-h)^2 + (y-k)^2 = r^2$. Since the circle passes through the point $(1,0)$, the distance from the center $(h,k)$ to $(1,0)$ is the radius $r$. $r^2 = (h-1)^2 + (k-0)^2 = (h-1)^2 + k^2$.

The circle is tangent to the curve $y=x$, which can be written as the line $x-y=0$. The distance from the center $(h,k)$ to the line $x-y=0$ is also the radius $r$. Using the formula for the distance from a point $(x_0, y_0)$ to a line $Ax+By+C=0$, which is $\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$: $r = \frac{|h-k|}{\sqrt{1^2+(-1)^2}} = \frac{|h-k|}{\sqrt{2}}$. Squaring this, we get $r^2 = \frac{(h-k)^2}{2}$.

Equating the two expressions for $r^2$: $(h-1)^2 + k^2 = \frac{(h-k)^2}{2}$ $2[(h-1)^2 + k^2] = (h-k)^2$ $2[h^2 - 2h + 1 + k^2] = h^2 - 2hk + k^2$ $2h^2 - 4h + 2 + 2k^2 = h^2 - 2hk + k^2$ Rearranging the terms to find the locus of $(h,k)$: $h^2 + 2hk + k^2 - 4h + 2 = 0$

Replacing $(h,k)$ with $(x,y)$ for the locus: $x^2 + 2xy + y^2 - 4x + 2 = 0$ This equation can be written as $(x+y)^2 - 4x + 2 = 0$. This is the equation of a parabola because the term $(x+y)^2$ indicates a rotation of axes. The discriminant $B^2-4AC = (2)^2 - 4(1)(1) = 0$.

To analyze the parabola, we use a rotation of axes by $\theta = \frac{\pi}{4}$. Let $X = \frac{x+y}{\sqrt{2}}$ and $Y = \frac{y-x}{\sqrt{2}}$. Then $x+y = \sqrt{2}X$. And $x = \frac{X-Y}{\sqrt{2}}$, $y = \frac{X+Y}{\sqrt{2}}$.

Substitute $x+y = \sqrt{2}X$ into the equation: $(\sqrt{2}X)^2 - 4x + 2 = 0$ $2X^2 - 4x + 2 = 0$ $X^2 - 2x + 1 = 0$

Now substitute $x = \frac{X-Y}{\sqrt{2}}$: $X^2 - 2\left(\frac{X-Y}{\sqrt{2}}\right) + 1 = 0$ $X^2 - \sqrt{2}(X-Y) + 1 = 0$ $X^2 - \sqrt{2}X + \sqrt{2}Y + 1 = 0$

To bring this into standard parabolic form, we complete the square for $X$: $(X^2 - \sqrt{2}X) + \sqrt{2}Y + 1 = 0$ $\left(X - \frac{\sqrt{2}}{2}\right)^2 - \left(\frac{\sqrt{2}}{2}\right)^2 + \sqrt{2}Y + 1 = 0$ $\left(X - \frac{1}{\sqrt{2}}\right)^2 - \frac{1}{2} + \sqrt{2}Y + 1 = 0$ $\left(X - \frac{1}{\sqrt{2}}\right)^2 + \sqrt{2}Y + \frac{1}{2} = 0$ $\left(X - \frac{1}{\sqrt{2}}\right)^2 = -\sqrt{2}Y - \frac{1}{2}$ $\left(X - \frac{1}{\sqrt{2}}\right)^2 = -\sqrt{2}\left(Y + \frac{1}{2\sqrt{2}}\right)$ $\left(X - \frac{1}{\sqrt{2}}\right)^2 = -\sqrt{2}\left(Y + \frac{\sqrt{2}}{4}\right)$

This equation is in the standard form $(X-h')^2 = 4a(Y-k')$, where $(h', k')$ is the vertex in the $(X,Y)$ system, and $4a$ is the parameter. Here, $h' = \frac{1}{\sqrt{2}}$, $k' = -\frac{\sqrt{2}}{4}$, and $4a = -\sqrt{2}$.

(A) Length of the latus rectum is $|4a| = |-\sqrt{2}| = \sqrt{2}$. This contradicts the option. (B) The axis of symmetry in the $(X,Y)$ system is $X = h'$, which is $X = \frac{1}{\sqrt{2}}$. Since $X = \frac{x+y}{\sqrt{2}}$, we substitute this back: $\frac{x+y}{\sqrt{2}} = \frac{1}{\sqrt{2}} \implies x+y = 1$. This option is correct. (C) The vertex in the $(X,Y)$ system is $(h', k') = (\frac{1}{\sqrt{2}}, -\frac{\sqrt{2}}{4})$. Converting back to $(x,y)$ coordinates: $x_v = \frac{X-Y}{\sqrt{2}} = \frac{\frac{1}{\sqrt{2}} - (-\frac{\sqrt{2}}{4})}{\sqrt{2}} = \frac{\frac{1}{\sqrt{2}} + \frac{\sqrt{2}}{4}}{\sqrt{2}} = \frac{1}{2} + \frac{1}{4} = \frac{3}{4}$. $y_v = \frac{X+Y}{\sqrt{2}} = \frac{\frac{1}{\sqrt{2}} + (-\frac{\sqrt{2}}{4})}{\sqrt{2}} = \frac{\frac{1}{\sqrt{2}} - \frac{\sqrt{2}}{4}}{\sqrt{2}} = \frac{1}{2} - \frac{1}{4} = \frac{1}{4}$. The vertex is $(\frac{3}{4}, \frac{1}{4})$. This option is correct. (D) The directrix in the $(X,Y)$ system is $Y = k' - a$. We have $k' = -\frac{\sqrt{2}}{4}$ and $4a = -\sqrt{2}$, so $a = -\frac{\sqrt{2}}{4}$. The directrix is $Y = -\frac{\sqrt{2}}{4} - (-\frac{\sqrt{2}}{4}) = 0$. Converting $Y=0$ back to $(x,y)$ coordinates: $Y = \frac{y-x}{\sqrt{2}}$, so $\frac{y-x}{\sqrt{2}} = 0 \implies y-x = 0 \implies x-y=0$. This option is correct.