Question

A board is being moved with a cosntant velocity $v_0$ on a smooth horizontal plane. A small block is projected on the rough boards. Coefficient of friction between board and block is $\mu$=0.3. Block is projected with velocity $v_1$ = 25 m/s at an angle of $\theta$=37° relative to ground. What is the velocity of block (in m/s) relative to ground after time t= 10 sec.

Answer 1

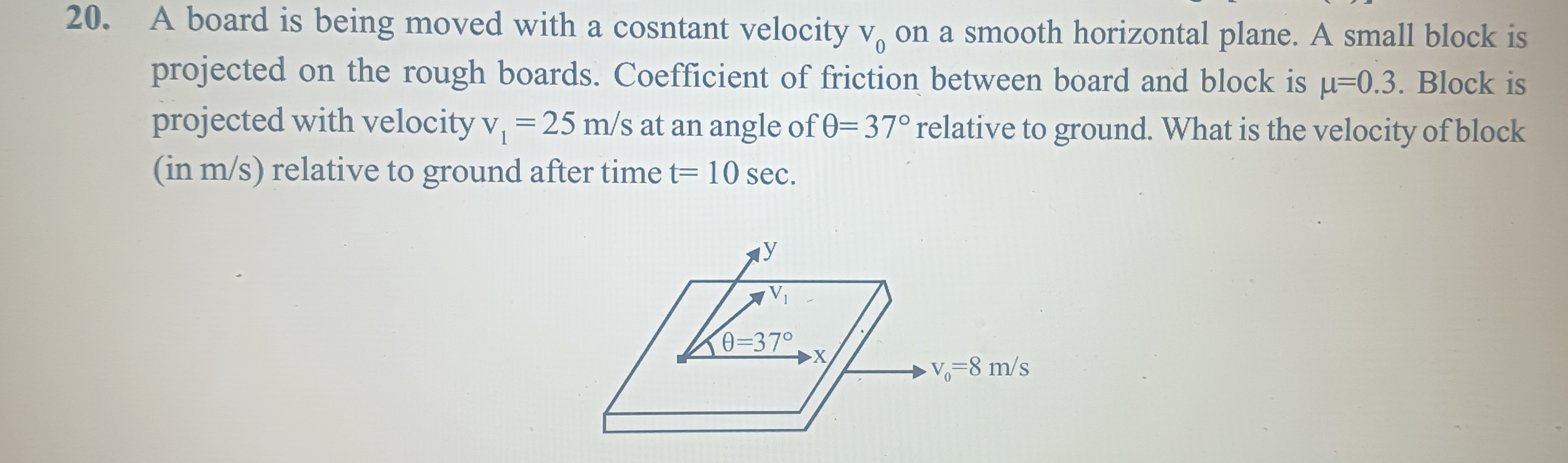
8 m/s

Answer 2

The problem involves a block sliding on a moving board with friction. We need to find the block's velocity relative to the ground after a specific time.

1. Define Coordinate System and Initial Velocities: Let the x-axis be in the direction of the board's motion. The velocity of the board relative to the ground is $\vec{v}_{board} = 8 \hat{i}$ m/s. The initial velocity of the block relative to the ground is $v_1 = 25$ m/s at an angle $\theta = 37^\circ$ to the x-axis. The components of the block's initial velocity relative to the ground are: $v_{block,g,x}(0) = v_1 \cos 37^\circ = 25 \times 0.8 = 20$ m/s $v_{block,g,y}(0) = v_1 \sin 37^\circ = 25 \times 0.6 = 15$ m/s So, $\vec{v}_{block,g}(0) = (20 \hat{i} + 15 \hat{j})$ m/s.

2. Calculate Initial Velocity of Block Relative to Board: The relative velocity of the block with respect to the board is: $\vec{v}_{block/board}(0) = \vec{v}_{block,g}(0) - \vec{v}_{board}$ $\vec{v}_{block/board}(0) = (20 \hat{i} + 15 \hat{j}) - 8 \hat{i} = (12 \hat{i} + 15 \hat{j})$ m/s.

3. Determine Friction Force and Block's Acceleration: The normal force on the block is $N = mg$. The kinetic friction force is $f_k = \mu N = \mu mg$. The coefficient of friction $\mu = 0.3$. So, $f_k = 0.3 mg$. The friction force opposes the relative motion. The direction of the friction force is opposite to $\vec{v}_{block/board}(0)$. The unit vector in the direction of relative motion is: $\hat{u}_{rel} = \frac{\vec{v}_{block/board}(0)}{|\vec{v}_{block/board}(0)|} = \frac{12 \hat{i} + 15 \hat{j}}{\sqrt{12^2 + 15^2}} = \frac{12 \hat{i} + 15 \hat{j}}{\sqrt{144 + 225}} = \frac{12 \hat{i} + 15 \hat{j}}{\sqrt{369}}$ Since $\sqrt{369} = \sqrt{9 \times 41} = 3\sqrt{41}$, $\hat{u}_{rel} = \frac{12 \hat{i} + 15 \hat{j}}{3\sqrt{41}} = \frac{4 \hat{i} + 5 \hat{j}}{\sqrt{41}}$. The acceleration of the block relative to the ground, due to friction, is $\vec{a}_{block,g} = \frac{\vec{f}_k}{m}$. $\vec{a}_{block,g} = -\frac{\mu mg}{m} \hat{u}_{rel} = -\mu g \hat{u}_{rel}$ Using $g = 10$ m/s$^2$: $\vec{a}_{block,g} = -(0.3)(10) \frac{4 \hat{i} + 5 \hat{j}}{\sqrt{41}} = -3 \frac{4 \hat{i} + 5 \hat{j}}{\sqrt{41}}$ m/s$^2$. Since the board moves at a constant velocity, its acceleration is zero ($\vec{a}_{board} = 0$). Therefore, the acceleration of the block relative to the board is the same as its acceleration relative to the ground: $\vec{a}_{block/board} = \vec{a}_{block,g}$.

4. Calculate Time for Relative Motion to Stop: The block stops sliding relative to the board when its relative velocity becomes zero. $\vec{v}_{block/board}(t) = \vec{v}_{block/board}(0) + \vec{a}_{block/board} t$ Set $\vec{v}_{block/board}(t) = 0$: $0 = (12 \hat{i} + 15 \hat{j}) - 3 \frac{4 \hat{i} + 5 \hat{j}}{\sqrt{41}} t_s$ $(12 \hat{i} + 15 \hat{j}) = 3 \frac{4 \hat{i} + 5 \hat{j}}{\sqrt{41}} t_s$ Dividing by 3: $(4 \hat{i} + 5 \hat{j}) = \frac{4 \hat{i} + 5 \hat{j}}{\sqrt{41}} t_s$ This implies $t_s = \sqrt{41}$ seconds. Numerically, $\sqrt{41} \approx 6.403$ seconds.

5. Determine Block's Velocity at t = 10 seconds: The time given is $t = 10$ seconds. Since $t = 10$ seconds is greater than $t_s \approx 6.403$ seconds, the block will have stopped sliding on the board by $t = 10$ seconds. Once the block stops sliding, it moves along with the board, meaning its velocity relative to the ground becomes equal to the board's velocity. Therefore, for $t \ge t_s$, the velocity of the block relative to the ground is $\vec{v}_{block,g}(t) = \vec{v}_{board} = 8 \hat{i}$ m/s.

At $t = 10$ sec, the velocity of the block relative to the ground is $8 \hat{i}$ m/s. The magnitude of this velocity is 8 m/s.