Question

y-1=m(x-3) and y-3=m(x-1) are two family of straight lines, at right angled to each other. The locus of their point of intersection is

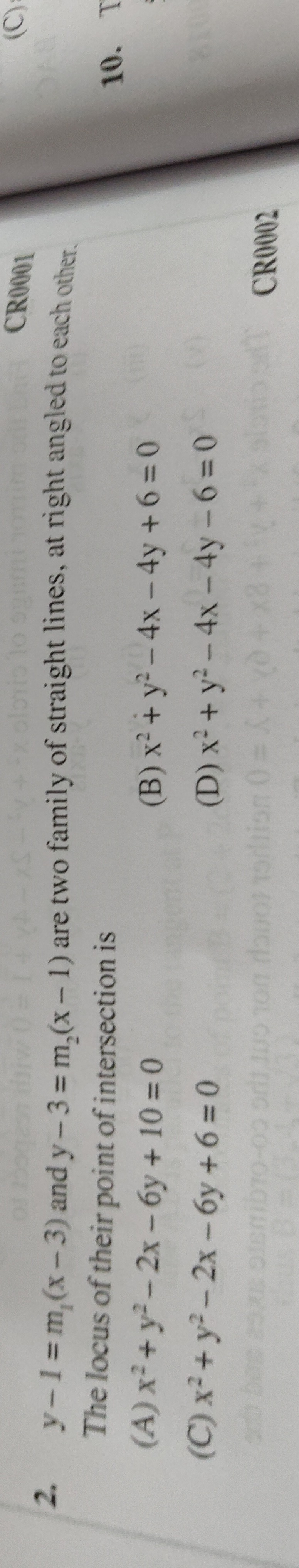
• A. x² + y²-2x - 6y + 10 = 0
• B. x² + y²-4x-4y + 6 = 0
• C. x² + y²-2x - 6y + 6 = 0
• D. x² + y²-4x-4y-6=0

Answer 1

Answer: (B)

x² + y²-4x-4y + 6 = 0

Answer 2

The two families of lines are given by $y - 1 = m(x - 3)$ and $y - 3 = m(x - 1)$. The first equation represents lines passing through the fixed point $A(3, 1)$. The second equation represents lines passing through the fixed point $B(1, 3)$. The condition that the lines are at right angles means that for any point of intersection $(x, y)$, the line segment from $(x, y)$ to $A(3, 1)$ is perpendicular to the line segment from $(x, y)$ to $B(1, 3)$.

The slope of the line segment connecting $(x, y)$ to $A(3, 1)$ is $m_1 = \frac{y-1}{x-3}$ (for $x \neq 3$). The slope of the line segment connecting $(x, y)$ to $B(1, 3)$ is $m_2 = \frac{y-3}{x-1}$ (for $x \neq 1$).

For perpendicular lines, the product of their slopes is $-1$: $m_1 m_2 = -1$ $\left(\frac{y-1}{x-3}\right) \left(\frac{y-3}{x-1}\right) = -1$ Multiply both sides by $(x-3)(x-1)$: $(y-1)(y-3) = -(x-3)(x-1)$ Expand both sides: $y^2 - 4y + 3 = -(x^2 - 4x + 3)$ $y^2 - 4y + 3 = -x^2 + 4x - 3$ Rearrange the terms to form the locus equation: $x^2 - 4x + y^2 - 4y + 3 + 3 = 0$ $x^2 + y^2 - 4x - 4y + 6 = 0$ This is the equation of a circle. Geometrically, this circle has the line segment connecting the two fixed points $A(3, 1)$ and $B(1, 3)$ as its diameter. The equation of a circle with diameter endpoints $(x_1, y_1)$ and $(x_2, y_2)$ is $(x-x_1)(x-x_2) + (y-y_1)(y-y_2) = 0$. Using $(3, 1)$ and $(1, 3)$: $(x-3)(x-1) + (y-1)(y-3) = 0$ $x^2 - 4x + 3 + y^2 - 4y + 3 = 0$ $x^2 + y^2 - 4x - 4y + 6 = 0$ This matches option (B).