Question

Write down the equations to normal at the ends of the latus rectum of the parabola $y^2 = 4a(x-a)$.

Answer 1

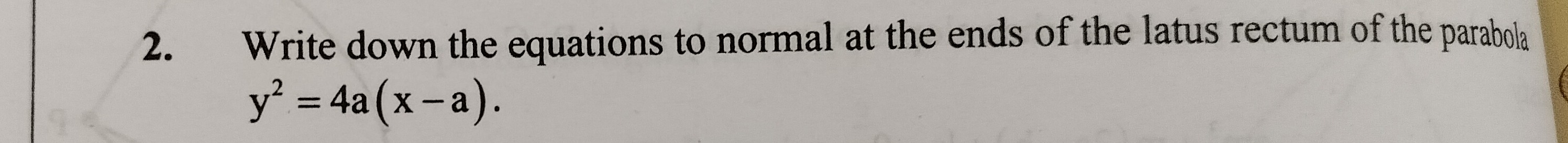
The equations of the normals at the ends of the latus rectum are $x + y = 4a$ and $x - y = 4a$.

Answer 2

The given parabola is $y^2 = 4a(x-a)$. This equation represents a parabola with its vertex shifted. Comparing it with the standard form $(y-k)^2 = 4A(x-h)$, we have: Vertex $(h, k) = (a, 0)$. Focal length $A = a$. The axis of symmetry is $y=k$, which is $y=0$. The parabola opens to the right. The focus of the parabola is at $(h+A, k) = (a+a, 0) = (2a, 0)$. The latus rectum is the chord passing through the focus and perpendicular to the axis of symmetry. Since the axis is $y=0$, the latus rectum lies on the vertical line $x = 2a$. To find the coordinates of the ends of the latus rectum, substitute $x=2a$ into the parabola's equation: $y^2 = 4a(2a - a) \implies y^2 = 4a^2 \implies y = \pm 2a$. So, the ends of the latus rectum are $L(2a, 2a)$ and $L'(2a, -2a)$. To find the equations of the normals at these points, we first find the slope of the tangent. Differentiating the parabola equation $y^2 = 4a(x-a)$ implicitly with respect to $x$: $2y \frac{dy}{dx} = 4a \implies \frac{dy}{dx} = \frac{2a}{y}$. For the point $L(2a, 2a)$: The slope of the tangent $m_t$ is $\frac{2a}{2a} = 1$. The slope of the normal $m_n$ is the negative reciprocal of the tangent's slope: $m_n = -\frac{1}{m_t} = -1$. The equation of the normal at $L(2a, 2a)$ using the point-slope form ($y - y_1 = m(x - x_1)$) is: $y - 2a = -1(x - 2a) \implies y - 2a = -x + 2a \implies x + y = 4a$. For the point $L'(2a, -2a)$: The slope of the tangent $m'_t$ is $\frac{2a}{-2a} = -1$. The slope of the normal $m'_n$ is $m'_n = -\frac{1}{m'_t} = 1$. The equation of the normal at $L'(2a, -2a)$ is: $y - (-2a) = 1(x - 2a) \implies y + 2a = x - 2a \implies x - y = 4a$. Therefore, the equations of the normals at the ends of the latus rectum are $x+y=4a$ and $x-y=4a$.