Solveeit Logo
Login

Question

Question: What will be the projection of vector $\vec{A}$ = $\hat{i}$+$\hat{j}$+$\hat{k}$ on vector $\vec{B}$ ...

What will be the projection of vector A⃗\vec{A} = i^\hat{i}+j^\hat{j}+k^\hat{k} on vector B⃗\vec{B} = i^\hat{i}+j^\hat{j} ? [JEE-Main-2021_July]

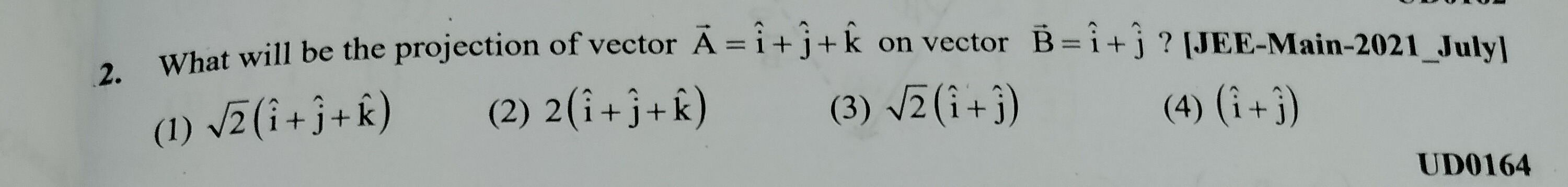
A

2\sqrt{2}(i^\hat{i}+j^\hat{j}+k^\hat{k})

B

2(i^\hat{i}+j^\hat{j}+k^\hat{k})

C

2\sqrt{2}(i^\hat{i}+j^\hat{j})

D

(i^\hat{i}+j^\hat{j})

Answer

(i^\hat{i}+j^\hat{j})

Explanation

Solution

The projection of vector A⃗\vec{A} on vector B⃗\vec{B} is given by the formula:

ProjB⃗A⃗=A⃗⋅B⃗∣B⃗∣2B⃗\text{Proj}_{\vec{B}}\vec{A} = \frac{\vec{A} \cdot \vec{B}}{|\vec{B}|^2} \vec{B}

Given vectors are A⃗=i^+j^+k^\vec{A} = \hat{i} + \hat{j} + \hat{k} and B⃗=i^+j^\vec{B} = \hat{i} + \hat{j}.

First, calculate the dot product A⃗⋅B⃗\vec{A} \cdot \vec{B}:

A⃗⋅B⃗=(i^+j^+k^)⋅(i^+j^)=(1)(1)+(1)(1)+(1)(0)=1+1+0=2\vec{A} \cdot \vec{B} = (\hat{i} + \hat{j} + \hat{k}) \cdot (\hat{i} + \hat{j}) = (1)(1) + (1)(1) + (1)(0) = 1 + 1 + 0 = 2

Next, calculate the magnitude squared of vector B⃗\vec{B}:

∣B⃗∣2=∣i^+j^∣2=(1)2+(1)2+(0)2=1+1=2|\vec{B}|^2 = |\hat{i} + \hat{j}|^2 = (1)^2 + (1)^2 + (0)^2 = 1 + 1 = 2

Now, substitute these values into the projection formula:

ProjB⃗A⃗=22(i^+j^)=1(i^+j^)=i^+j^\text{Proj}_{\vec{B}}\vec{A} = \frac{2}{2} (\hat{i} + \hat{j}) = 1 (\hat{i} + \hat{j}) = \hat{i} + \hat{j}

Thus, the projection of vector A⃗\vec{A} on vector B⃗\vec{B} is i^+j^\hat{i} + \hat{j}.