Solveeit Logo
Login

Question

Question: $\vec{A} + \vec{B} = 2\hat{i}$ and $\vec{A} - \vec{B} = 4\hat{j}$ then angle between $\vec{A}$ and $...

A⃗+B⃗=2i^\vec{A} + \vec{B} = 2\hat{i} and A⃗−B⃗=4j^\vec{A} - \vec{B} = 4\hat{j} then angle between A⃗\vec{A} and B⃗\vec{B} is :-

A

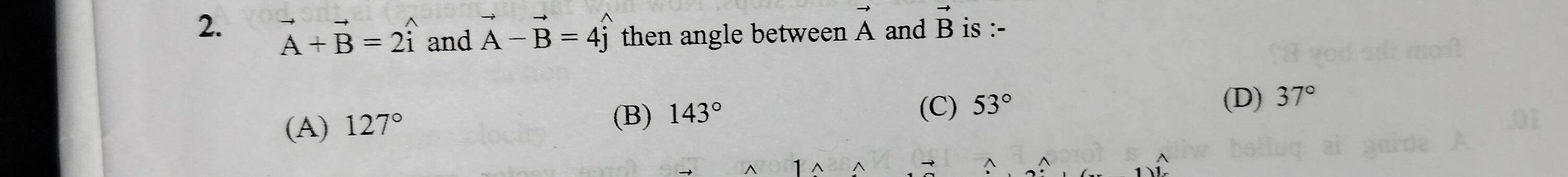
127°

B

143°

C

53°

D

37°

Answer

127°

Explanation

Solution

To find the angle between vectors A⃗\vec{A} and B⃗\vec{B}, we first need to determine the vectors themselves. Given the equations:

  1. A⃗+B⃗=2i^\vec{A} + \vec{B} = 2\hat{i}
  2. A⃗−B⃗=4j^\vec{A} - \vec{B} = 4\hat{j}

Adding the two equations:

2A⃗=2i^+4j^2\vec{A} = 2\hat{i} + 4\hat{j} A⃗=i^+2j^\vec{A} = \hat{i} + 2\hat{j}

Subtracting the second equation from the first:

2B⃗=2i^−4j^2\vec{B} = 2\hat{i} - 4\hat{j} B⃗=i^−2j^\vec{B} = \hat{i} - 2\hat{j}

Now, we use the dot product formula to find the angle θ\theta between A⃗\vec{A} and B⃗\vec{B}:

A⃗⋅B⃗=∣A⃗∣∣B⃗∣cos⁡θ\vec{A} \cdot \vec{B} = |\vec{A}| |\vec{B}| \cos\theta

cos⁡θ=A⃗⋅B⃗∣A⃗∣∣B⃗∣\cos\theta = \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| |\vec{B}|}

Calculate the dot product:

A⃗⋅B⃗=(i^+2j^)⋅(i^−2j^)=(1)(1)+(2)(−2)=1−4=−3\vec{A} \cdot \vec{B} = (\hat{i} + 2\hat{j}) \cdot (\hat{i} - 2\hat{j}) = (1)(1) + (2)(-2) = 1 - 4 = -3

Calculate the magnitudes:

∣A⃗∣=12+22=5|\vec{A}| = \sqrt{1^2 + 2^2} = \sqrt{5} ∣B⃗∣=12+(−2)2=5|\vec{B}| = \sqrt{1^2 + (-2)^2} = \sqrt{5}

Substitute into the cosine formula:

cos⁡θ=−35⋅5=−35\cos\theta = \frac{-3}{\sqrt{5} \cdot \sqrt{5}} = \frac{-3}{5}

Find the angle θ\theta:

θ=arccos⁡(−35)\theta = \arccos\left(-\frac{3}{5}\right)

Since cos⁡θ\cos\theta is negative, θ\theta lies in the second quadrant. The reference angle α\alpha such that cos⁡α=35\cos\alpha = \frac{3}{5} is approximately 53∘53^\circ.

Therefore, θ=180∘−53∘=127∘\theta = 180^\circ - 53^\circ = 127^\circ.