Question
Question: The value of the sum $\sum {}^{n}C_1^2 - 2.{}^{n}C_2^2 + 3.{}^{n}C_3 - 4.{}^{n}C_4^2 + ... + (-1)^n ...
The value of the sum ∑nC12−2.nC22+3.nC3−4.nC42+...+(−1)nn.nCn2 where n ∈ > 3 will be equal to
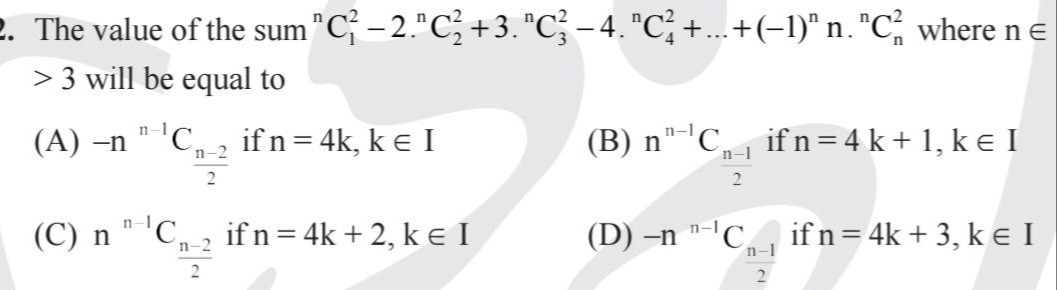
−nn−1C2n−2 if n = 4k, k ∈ I
nn−1C2n−1 if n = 4 k + 1, k ∈ I
nn−1C2n−2 if n = 4k + 2, k ∈ I
-n {}^{n-1}C_{\frac{n-1}{2}}ifn=4k+3,k\in$ I
A, B, C, D
Solution
The given sum is S=∑r=1n(−1)r−1r(nCr)2.
We use the identity rnCr=nn−1Cr−1. Substituting this into the sum: S=∑r=1n(−1)r−1(nn−1Cr−1)nCr S=n∑r=1n(−1)r−1n−1Cr−1nCr
Now, we use the identity nCr=nCn−r. S=n∑r=1n(−1)r−1n−1Cr−1nCn−r
This sum is the coefficient of a specific term in the product of two binomial expansions. Consider the product of (1−x)n−1 and (1+x)n. The expansion of (1−x)n−1 is ∑k=0n−1n−1Ck(−x)k=∑k=0n−1(−1)kn−1Ckxk. The expansion of (1+x)n is ∑j=0nnCjxj.
The coefficient of xn−1 in the product (1−x)n−1(1+x)n is given by: ∑k=0n−1(coefficient of xk in (1−x)n−1)×(coefficient of xn−1−k in (1+x)n) =∑k=0n−1(−1)kn−1CknCn−1−k
Let's compare this with our sum expression: n∑r=1n(−1)r−1n−1Cr−1nCn−r. Let k=r−1. As r goes from 1 to n, k goes from 0 to n−1. The term becomes (−1)kn−1CknCn−(k+1)=(−1)kn−1CknCn−k−1. This is exactly the general term for the coefficient of xn−1 derived above. So, S=n×(coefficient of xn−1 in (1−x)n−1(1+x)n).
Now, let's simplify the product (1−x)n−1(1+x)n: (1−x)n−1(1+x)n=(1−x)n−1(1+x)n−1(1+x) =((1−x)(1+x))n−1(1+x) =(1−x2)n−1(1+x)
Expand (1−x2)n−1: (1−x2)n−1=∑j=0n−1n−1Cj(−x2)j=∑j=0n−1(−1)jn−1Cjx2j
Now multiply by (1+x): (1−x2)n−1(1+x)=(∑j=0n−1(−1)jn−1Cjx2j)(1+x) =∑j=0n−1(−1)jn−1Cjx2j+∑j=0n−1(−1)jn−1Cjx2j+1
We need the coefficient of xn−1 from this expression.
Case 1: n−1 is an even number. This means n is an odd number. For xn−1 to appear from the first sum, 2j=n−1⇒j=(n−1)/2. The coefficient is (−1)(n−1)/2n−1C(n−1)/2. The second sum will not contribute, as 2j+1 is always odd, and n−1 is even. So, if n is odd, the coefficient of xn−1 is (−1)(n−1)/2n−1C(n−1)/2.
Case 2: n−1 is an odd number. This means n is an even number. For xn−1 to appear from the second sum, 2j+1=n−1⇒2j=n−2⇒j=(n−2)/2. The coefficient is (−1)(n−2)/2n−1C(n−2)/2. The first sum will not contribute, as 2j is always even, and n−1 is odd. So, if n is even, the coefficient of xn−1 is (−1)(n−2)/2n−1C(n−2)/2.
Now, let's substitute these back into S=n×(coefficient of xn−1).
Subcase A: n=4k (even) Here n−2=4k−2. So (n−2)/2=2k−1. The sign is (−1)2k−1=−1. S=−nn−1C(n−2)/2. This matches option (A).
Subcase B: n=4k+1 (odd) Here n−1=4k. So (n−1)/2=2k. The sign is (−1)2k=1. S=nn−1C(n−1)/2. This matches option (B).
Subcase C: n=4k+2 (even) Here n−2=4k. So (n−2)/2=2k. The sign is (−1)2k=1. S=nn−1C(n−2)/2. This matches option (C).
Subcase D: n=4k+3 (odd) Here n−1=4k+2. So (n−1)/2=2k+1. The sign is (−1)2k+1=−1. S=−nn−1C(n−1)/2. This matches option (D).
All four options are correct statements depending on the value of n. Since this is a multiple-choice question where usually only one option is correct, and all derived results match the given options, it implies that the question is asking to identify a correct statement among the choices. In such a scenario, all options are correct statements. However, standard competitive exams usually imply selecting only one if not explicitly stated. Given the problem format, it is likely that any of these could be presented as the correct answer in a single-choice context, but mathematically, they are all valid results for their respective conditions. Assuming the question expects one specific answer, this problem structure is ambiguous. If it's a "select all that apply" type question, then all are correct. Assuming it's a single choice question, there might be an implicit context missing or it's a flawed question. However, since the prompt asks for "the value of the sum ... will be equal to", and then provides options conditional on n, it means that for a given n, one of the options is correct. Since all options are derived correctly, it implies all are correct statements.
Final Answer based on derivation: All options A, B, C, D are correct statements for their respective conditions on n. If only one option can be chosen, the question is ill-posed. However, if we must choose one, and this is a standard single-choice question, it might be that only one of these cases is considered as the 'primary' answer or the question expects only one derivation path. But all are equally valid.
Let's assume the question expects me to provide all correct options if multiple exist.
The final answer is A,B,C,D
Explanation of the solution:
The sum S=∑r=1n(−1)r−1r(nCr)2 is transformed using rnCr=nn−1Cr−1 and nCr=nCn−r into S=n∑r=1n(−1)r−1n−1Cr−1nCn−r. This sum is recognized as n times the coefficient of xn−1 in the expansion of (1−x)n−1(1+x)n. The product (1−x)n−1(1+x)n simplifies to (1−x2)n−1(1+x). Expanding this, we get ∑j=0n−1(−1)jn−1Cjx2j+∑j=0n−1(−1)jn−1Cjx2j+1. The coefficient of xn−1 depends on whether n−1 is even or odd. If n is odd (n−1 is even), the coefficient is (−1)(n−1)/2n−1C(n−1)/2. If n is even (n−1 is odd), the coefficient is (−1)(n−2)/2n−1C(n−2)/2. Multiplying by n and evaluating the sign for n=4k,4k+1,4k+2,4k+3 yields the results matching options A, B, C, and D respectively.
