Question
Question: The temperature of a well stirred liquid kept open to a cold surrounding is plotted against time. Th...
The temperature of a well stirred liquid kept open to a cold surrounding is plotted against time. The value of sec2θ1 is :-
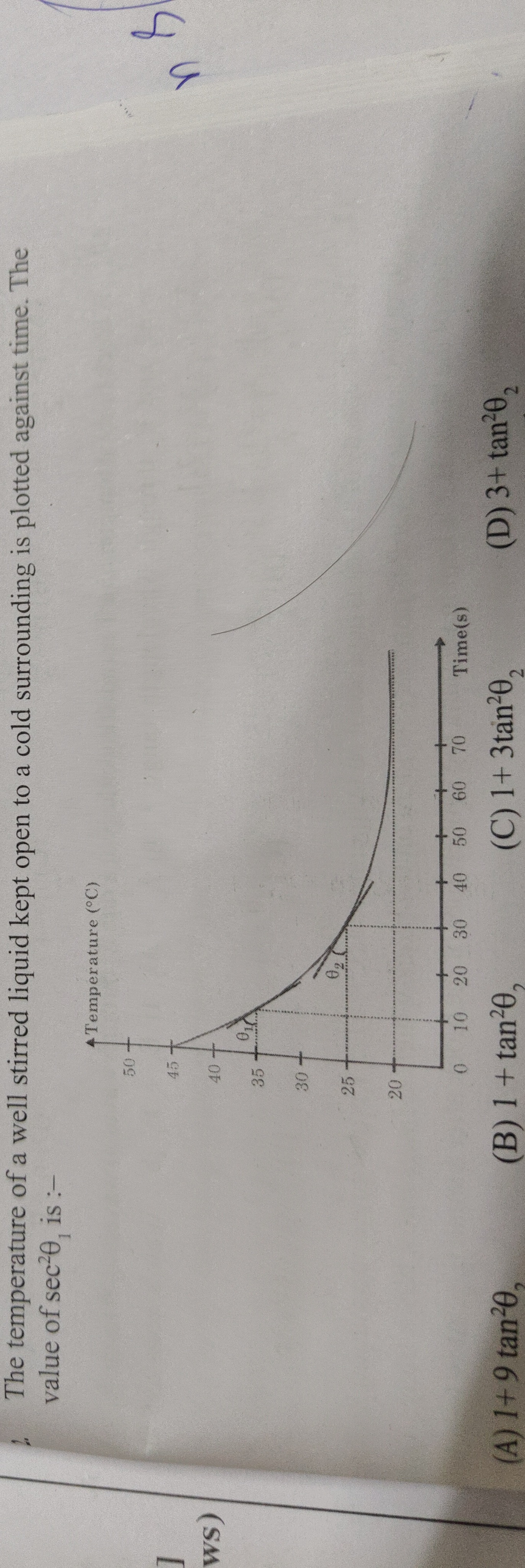
1+ 9 tan2θ1
1 + tan2θ1
1+ 3tan2θ2
3+ tan2θ2
1 + tan2θ1
Solution
Newton's Law of Cooling states that dtdT=−k(T−Ta), where T is the temperature of the liquid, t is time, Ta is the ambient temperature, and k is a positive constant. From the graph, we can infer that the ambient temperature Ta=20∘C. The slope of the tangent to the temperature-time curve at any point is given by dtdT. The angle θ1 is associated with the tangent at T=35∘C, so tanθ1=dtdTT=35∘C=−k(35−Ta)=−k(35−20)=−15k. The angle θ2 is associated with the tangent at T=30∘C, so tanθ2=dtdTT=30∘C=−k(30−Ta)=−k(30−20)=−10k. We are asked to find the value of sec2θ1. Using the fundamental trigonometric identity, sec2θ1=1+tan2θ1. This identity directly matches option (B). While we can derive a relationship between tanθ1 and tanθ2 (tanθ1=−10k−15ktanθ2=23tanθ2), and thus express sec2θ1 as 1+(23tanθ2)2=1+49tan2θ2, this expression is not among the options. Given that option (B) is a universally true trigonometric identity for sec2θ1, and the question asks for "the value of sec2θ1 is :-", the most appropriate answer is the identity itself, as it correctly represents sec2θ1. The other options represent different mathematical expressions that do not directly equate to sec2θ1 based on the provided information and standard identities.
