Question
Question: The tangent to the curve $y = x^2$ at point (1, 1) is:...
The tangent to the curve y=x2 at point (1, 1) is:
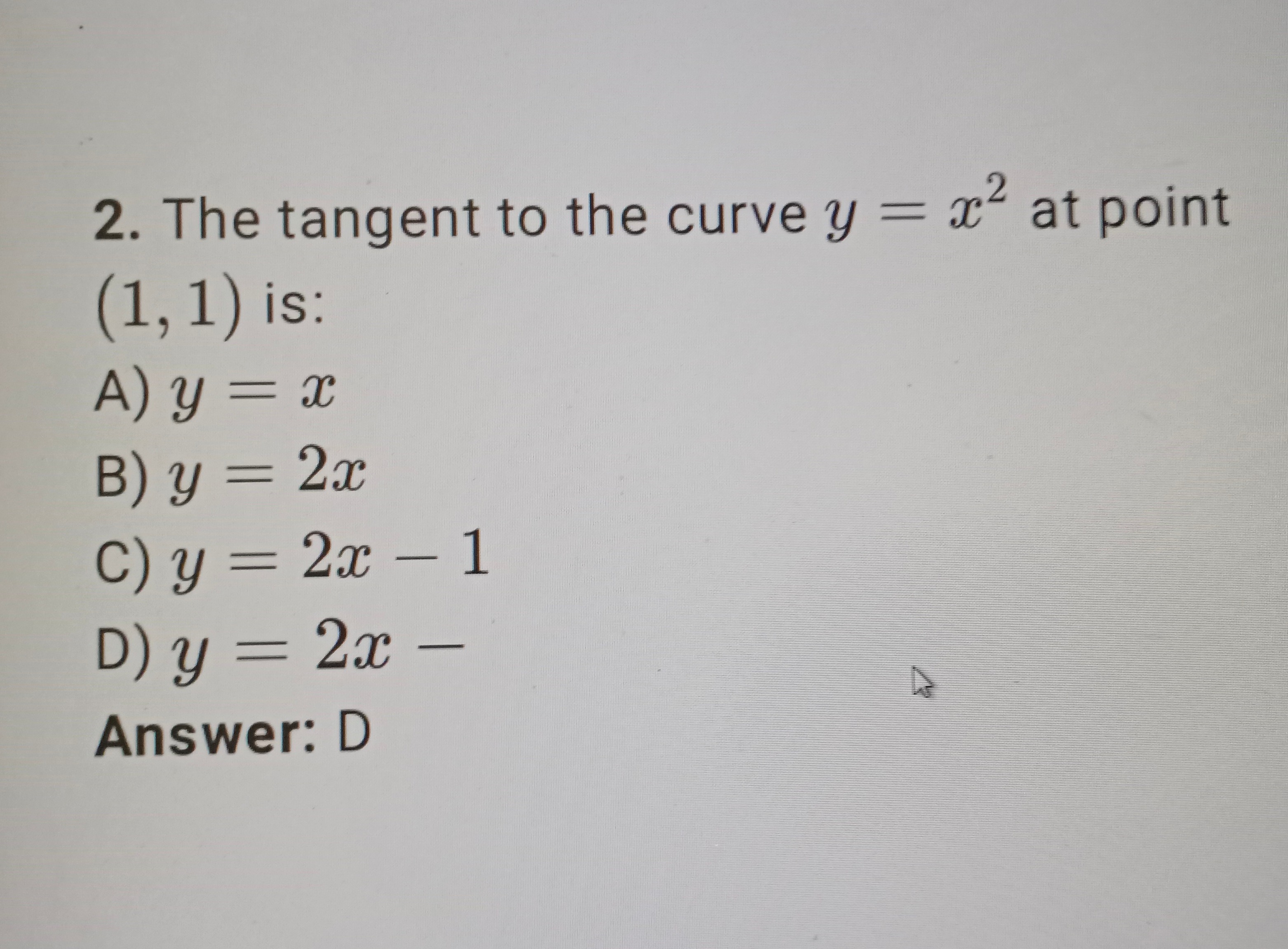
y=x
y=2x
y=2x−1
y=2x−
C) y=2x−1
Solution
To find the equation of the tangent line to the curve y=x2 at the point (1, 1), we follow these steps:
-
Find the derivative of the function y=x2. The derivative, denoted as dxdy, gives the slope of the tangent line at any point on the curve.
dxdy=2x -
Evaluate the derivative at the given point (1, 1) to find the slope of the tangent line at that specific point. Substitute x=1 into the derivative:
m=2(1)=2Thus, the slope of the tangent line at (1, 1) is 2.
-
Use the point-slope form of a linear equation to find the equation of the tangent line. The point-slope form is given by:
y−y1=m(x−x1)where (x1,y1) is the given point and m is the slope. Substituting (x1,y1)=(1,1) and m=2, we get:
y−1=2(x−1) -
Simplify the equation to obtain the equation of the tangent line in slope-intercept form:
y−1=2x−2 y=2x−1
Therefore, the equation of the tangent line to the curve y=x2 at the point (1, 1) is y=2x−1.
