Question
Question: The system of equations, $x+y+z=6, x+2y+3z = 10$ and $x + 2y + \lambda z = \mu$ has no solution, if...
The system of equations, x+y+z=6,x+2y+3z=10 and x+2y+λz=μ has no solution, if
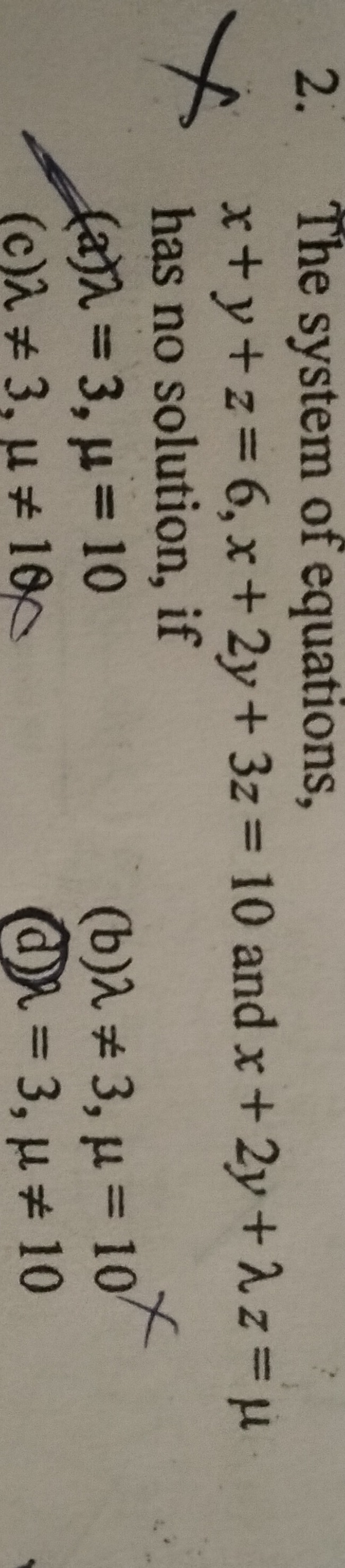
λ = 3, μ = 10
λ ≠ 3, μ = 10
λ ≠ 3, μ ≠ 10
λ = 3, μ≠ 10
λ = 3, μ≠ 10
Solution
The given system of equations is:
- x+y+z=6
- x+2y+3z=10
- x+2y+λz=μ
We can write the augmented matrix of the system as: [A∣B]=11112213λ∣∣∣610μ
We apply row operations to transform the matrix into row-echelon form. R2←R2−R1 R3←R3−R1 10011112λ−1∣∣∣64μ−6
R3←R3−R2 10011012(λ−1)−2∣∣∣64(μ−6)−4 10011012λ−3∣∣∣64μ−10
The corresponding system of equations is: x+y+z=6 y+2z=4 (λ−3)z=μ−10
For the system to have no solution, the last equation must be contradictory. This happens when the coefficient of z is zero, but the constant term on the right side is non-zero. So, we must have: λ−3=0⟹λ=3 and μ−10=0⟹μ=10
Thus, the system has no solution if λ=3 and μ=10.
Let's check the given options: (α) λ=3,μ=10: The last equation becomes 0⋅z=0, which means infinitely many solutions. (b) λ=3,μ=10: The last equation has a non-zero coefficient for z, so there is a unique solution for z, and consequently for x and y. (c) λ=3,μ=10: The last equation has a non-zero coefficient for z, so there is a unique solution for z, and consequently for x and y. (d) λ=3,μ=10: The last equation becomes 0⋅z=(non-zero number), which is a contradiction, meaning no solution exists.
The condition for no solution is λ=3 and μ=10.
