Question

The length of the intercept on y-axis cut off by the parabola, $y^2 - 5y = 3x - 6$ is

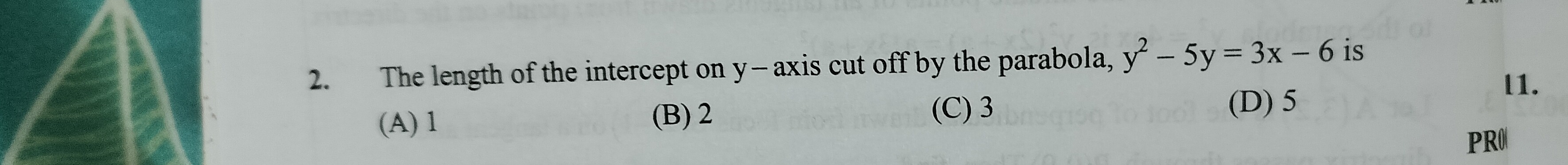
• A. 1
• B. 2
• C. 3
• D. 5

Answer 1

Answer: (A)

1

Answer 2

To find the intercept on the y-axis, we set $x = 0$ in the given equation of the parabola. The equation becomes $y^2 - 5y = 3(0) - 6$, which simplifies to $y^2 - 5y + 6 = 0$. Solving this quadratic equation for $y$ by factoring gives $(y - 2)(y - 3) = 0$. The roots are $y_1 = 2$ and $y_2 = 3$. These are the y-coordinates where the parabola intersects the y-axis. The length of the intercept on the y-axis is the absolute difference between these roots: $|y_2 - y_1| = |3 - 2| = 1$.