Question
Question: The figure represent a U-tube of uniform cross-section filled with two immiscible liquids. One is wa...
The figure represent a U-tube of uniform cross-section filled with two immiscible liquids. One is water with density ρw and other liquid is of density ρ. The liquid interface lies 2 cm above base. The relation between ρ and ρw is (assume that the level of liquid in two arms is same)
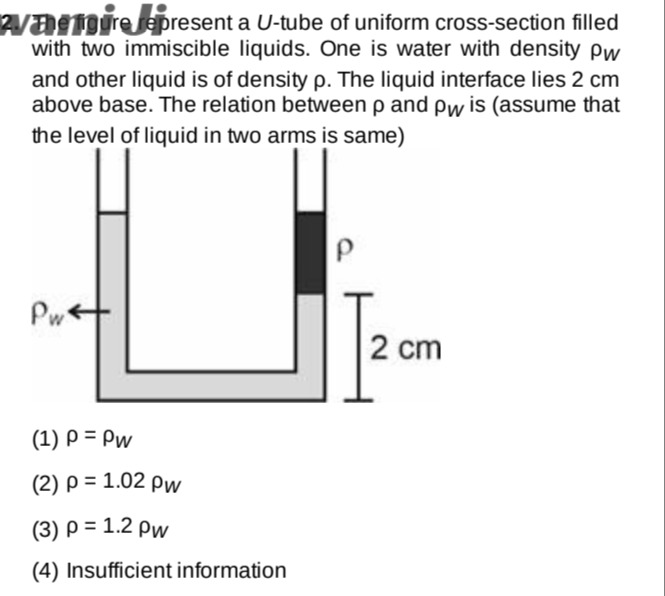
ρ=ρw
ρ=1.02ρw
ρ=1.2ρw
Insufficient information
ρ=ρw
Solution
Let the free surface level be at height h0 in both arms.
-
Left arm (only water):
Pressure at free surface = ρwgh0. -
Right arm:
The U-tube contains water from the base to 2 cm and liquid of density ρ above that up to h0.
Pressure at free surface = 2ρwg+(h0−2)ρg.
Since the free surfaces are at the same level, equate pressures:
ρwgh0=2ρwg+(h0−2)ρg.Cancel g and rearrange:
ρwh0=2ρw+ρ(h0−2). ρwh0−ρh0=2ρw−2ρ. h0(ρw−ρ)=2(ρw−ρ). (ρw−ρ)(h0−2)=0.Since h0=2 (otherwise, there would be no layer of liquid ρ), we must have
ρw−ρ=0⇒ρ=ρw.