Question

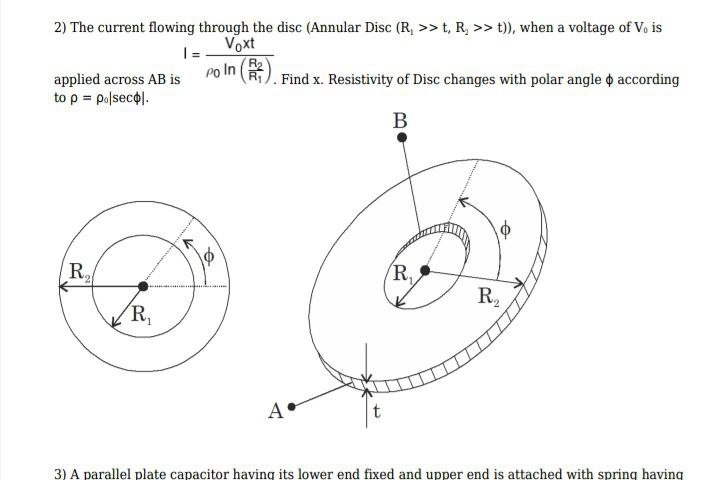
The current flowing through the disc (Annular Disc ($R_1 >> t, R_2 >> t$)), when a voltage of $V_0$ is $I = \frac{V_0xt}{\rho_0 ln(\frac{R_2}{R_1})}$. Find x. Resistivity of Disc changes with polar angle $\phi$ according applied across AB is to $\rho = \rho_0 |sec\phi|$.

Answer 1

4

Answer 2

The problem asks us to find the value of 'x' in the given expression for the current flowing through an annular disc. The resistivity of the disc varies with the polar angle $\phi$.

1. Identify the current flow path:

The voltage $V_0$ is applied across points A and B. From the diagram, A is on the outer edge (radius $R_2$) and B is on the inner edge (radius $R_1$), both seemingly at the same polar angle $\phi$. This implies that the current flows radially from the inner radius to the outer radius (or vice versa).

2. Consider an elementary radial strip:

Imagine dividing the annular disc into many thin radial strips, each of angular width $d\phi$ at a polar angle $\phi$. Since the voltage $V_0$ is applied across the inner and outer edges, all these radial strips are connected in parallel across the voltage $V_0$.

3. Calculate the resistance of an elementary radial strip:

For a small radial element of length $dr$ at radius $r$ and angle $\phi$, its cross-sectional area for current flow is $dA = (r d\phi) \cdot t$, where $t$ is the thickness of the disc. The resistivity at this angle $\phi$ is given by $\rho(\phi) = \rho_0 |\sec\phi|$. The resistance of this elementary radial segment $dR_{segment}$ is: $dR_{segment} = \rho(\phi) \frac{dr}{dA} = \frac{\rho_0 |\sec\phi| dr}{r t d\phi}$.

To find the total resistance of a full radial strip from $R_1$ to $R_2$ at a given angle $\phi$, we integrate $dR_{segment}$ from $R_1$ to $R_2$: $R_{strip}(\phi) = \int_{R_1}^{R_2} \frac{\rho_0 |\sec\phi| dr}{r t d\phi}$ $R_{strip}(\phi) = \frac{\rho_0 |\sec\phi|}{t d\phi} \int_{R_1}^{R_2} \frac{dr}{r}$ $R_{strip}(\phi) = \frac{\rho_0 |\sec\phi|}{t d\phi} [\ln r]_{R_1}^{R_2}$ $R_{strip}(\phi) = \frac{\rho_0 |\sec\phi|}{t d\phi} \ln\left(\frac{R_2}{R_1}\right)$.

4. Calculate the current through an elementary radial strip:

Since the voltage $V_0$ is applied across each strip, the current $dI$ flowing through an elementary strip at angle $\phi$ is given by Ohm's law: $dI = \frac{V_0}{R_{strip}(\phi)}$ $dI = \frac{V_0}{\frac{\rho_0 |\sec\phi|}{t d\phi} \ln\left(\frac{R_2}{R_1}\right)}$ $dI = \frac{V_0 t d\phi}{\rho_0 |\sec\phi| \ln\left(\frac{R_2}{R_1}\right)}$.

5. Calculate the total current:

To find the total current $I$ flowing through the entire disc, we integrate $dI$ over the full range of polar angles, from $\phi = 0$ to $\phi = 2\pi$: $I = \int_0^{2\pi} dI = \int_0^{2\pi} \frac{V_0 t d\phi}{\rho_0 |\sec\phi| \ln\left(\frac{R_2}{R_1}\right)}$ $I = \frac{V_0 t}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)} \int_0^{2\pi} \frac{d\phi}{|\sec\phi|}$ Since $\frac{1}{|\sec\phi|} = |\cos\phi|$, we have: $I = \frac{V_0 t}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)} \int_0^{2\pi} |\cos\phi| d\phi$.

6. Evaluate the integral:

The integral $\int_0^{2\pi} |\cos\phi| d\phi$ can be evaluated by considering the symmetry of $|\cos\phi|$. The function $|\cos\phi|$ is positive in $[0, \pi/2]$ and $[3\pi/2, 2\pi]$, and negative in $[\pi/2, 3\pi/2]$ (where $\cos\phi$ is negative, so $|\cos\phi|$ is positive). $\int_0^{2\pi} |\cos\phi| d\phi = \int_0^{\pi/2} \cos\phi d\phi + \int_{\pi/2}^{3\pi/2} (-\cos\phi) d\phi + \int_{3\pi/2}^{2\pi} \cos\phi d\phi$ $= [\sin\phi]_0^{\pi/2} + [-\sin\phi]_{\pi/2}^{3\pi/2} + [\sin\phi]_{3\pi/2}^{2\pi}$ $= (\sin(\pi/2) - \sin(0)) + (-\sin(3\pi/2) - (-\sin(\pi/2))) + (\sin(2\pi) - \sin(3\pi/2))$ $= (1 - 0) + (-(-1) - (-1)) + (0 - (-1))$ $= 1 + (1 + 1) + 1 = 4$. Alternatively, using symmetry, $\int_0^{2\pi} |\cos\phi| d\phi = 4 \int_0^{\pi/2} \cos\phi d\phi = 4 [\sin\phi]_0^{\pi/2} = 4(1-0) = 4$.

7. Substitute the integral value and find x:

Substituting the value of the integral back into the expression for $I$: $I = \frac{V_0 t}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)} \cdot 4$ $I = \frac{4 V_0 t}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)}$.

The problem states that the current is given by $I = \frac{V_0xt}{\rho_0 \ln(\frac{R_2}{R_1})}$. Comparing our derived expression with the given one: $\frac{4 V_0 t}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)} = \frac{V_0xt}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)}$ From this comparison, we can conclude that $x = 4$.

The final answer is $\boxed{4}$.

Explanation of the solution: The current flows radially. The annular disc is treated as a collection of parallel radial strips, each with a resistance dependent on its polar angle $\phi$.

1. Resistance of a radial strip: For a strip at angle $\phi$ and angular width $d\phi$, its resistance is $dR_{strip} = \frac{\rho_0 |\sec\phi|}{t d\phi} \ln\left(\frac{R_2}{R_1}\right)$.
2. Current through a strip: The voltage $V_0$ is applied across each strip, so $dI = \frac{V_0}{dR_{strip}} = \frac{V_0 t d\phi}{\rho_0 |\sec\phi| \ln\left(\frac{R_2}{R_1}\right)}$.
3. Total current: Integrate $dI$ from $\phi = 0$ to $2\pi$: $I = \frac{V_0 t}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)} \int_0^{2\pi} |\cos\phi| d\phi$.
4. Evaluate integral: $\int_0^{2\pi} |\cos\phi| d\phi = 4$.
5. Result: $I = \frac{4 V_0 t}{\rho_0 \ln\left(\frac{R_2}{R_1}\right)}$.
6. Compare: Comparing with the given formula $I = \frac{V_0xt}{\rho_0 \ln(\frac{R_2}{R_1})}$, we find $x=4$.