Question

Starting at temperature 300 K, one mole of an ideal diatomic gas ($\gamma$ = 1.4) is first compressed adiabatically from volume $V_1$ to $V_2 = \frac{V_1}{16}$. It is then allowed to expand isobarically to volume $2V_2$. If all the processes are the quasi-static, then the final temperature of the gas (in K) is (to the nearest integer) ____.

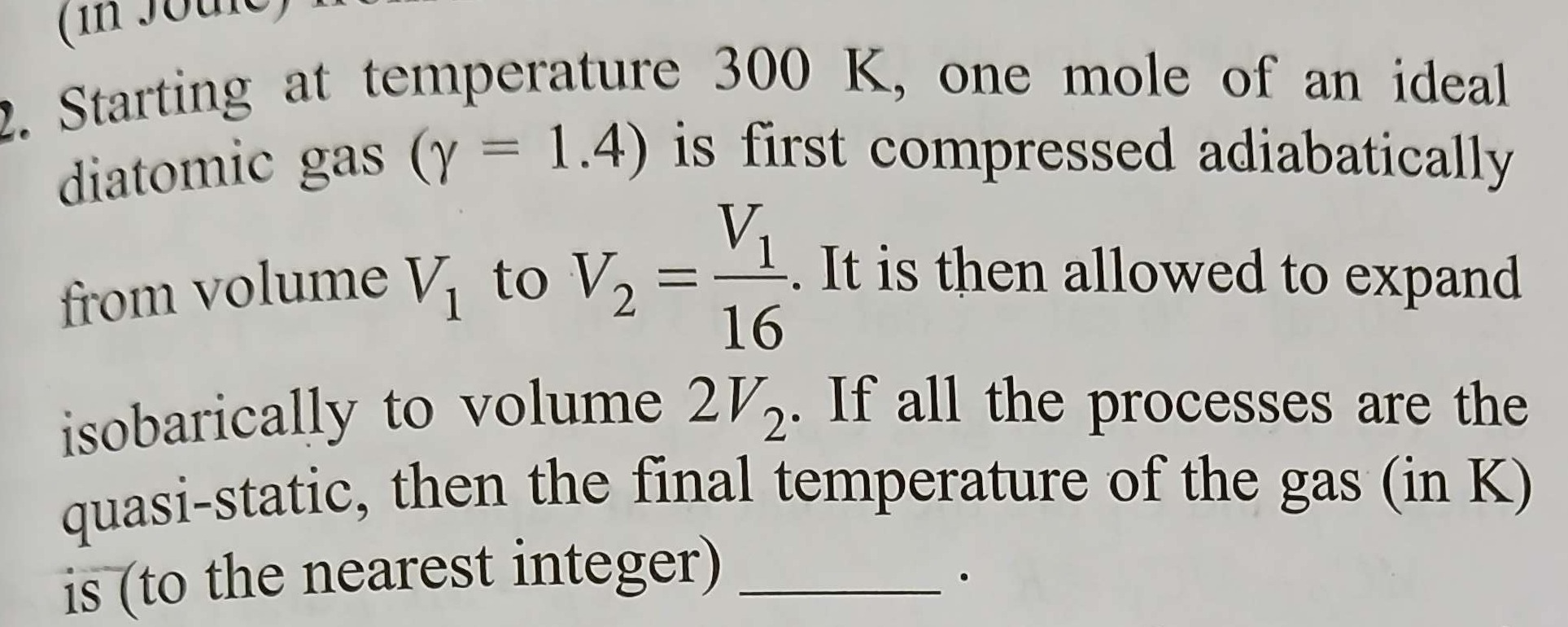
Answer 1

1819

Answer 2

1. Adiabatic Compression:
   For an adiabatic process,

   $$T V^{\gamma -1} = \text{constant}$$

   With initial $T_1 = 300\,\text{K}$ at volume $V_1$ and final volume $V_2 = \frac{V_1}{16}$, the temperature after compression is

   $$T_2 = T_1 \left(\frac{V_1}{V_2}\right)^{\gamma-1} = 300 \left(16\right)^{0.4}.$$

   Calculate $\left(16\right)^{0.4} = e^{0.4\ln16} \approx e^{1.109} \approx 3.031$.
   Thus,

   $$T_2 \approx 300 \times 3.031 \approx 909\,\text{K}.$$

2. Isobaric Expansion:
   Under constant pressure, temperature is directly proportional to volume. When volume is doubled from $V_2$ to $2V_2$:

   $$T_3 = T_2 \times 2 \approx 909 \times 2 \approx 1818\,\text{K}.$$

   Rounding to the nearest integer gives 1819 K.