Question

$\sec 1 \cdot \sec 2 + \sec 2 \cdot \sec 3 + \sec 3.\sec 4 + \dots$

Answer 1

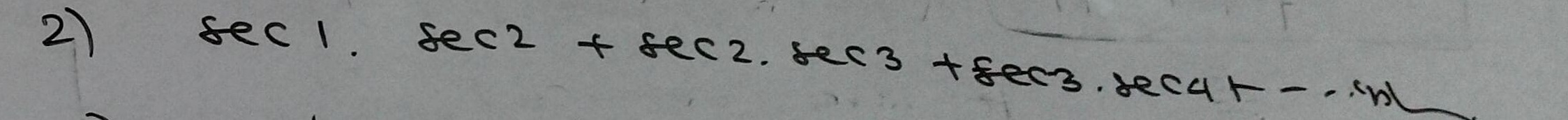
$\frac{\tan(n+1) - \tan 1}{\sin 1}$

Answer 2

To find the sum of the given series, we first identify the general term. The series is $\sec 1 \cdot \sec 2 + \sec 2 \cdot \sec 3 + \sec 3 \cdot \sec 4 + \dots$ The general term of the series can be written as $T_k = \sec k \cdot \sec(k+1)$. We can rewrite $\sec k$ as $\frac{1}{\cos k}$. So, $T_k = \frac{1}{\cos k \cdot \cos(k+1)}$.

To make this term suitable for a telescoping sum, we use the identity $\sin(A-B) = \sin A \cos B - \cos A \sin B$. Let $A = k+1$ and $B = k$. Then $A-B = (k+1) - k = 1$. So, $\sin((k+1)-k) = \sin 1$. We multiply and divide the general term by $\sin 1$: $T_k = \frac{1}{\sin 1} \cdot \frac{\sin((k+1)-k)}{\cos k \cdot \cos(k+1)}$

Now, expand the numerator using the sine difference identity: $T_k = \frac{1}{\sin 1} \cdot \frac{\sin(k+1)\cos k - \cos(k+1)\sin k}{\cos k \cdot \cos(k+1)}$ Separate the terms: $T_k = \frac{1}{\sin 1} \left( \frac{\sin(k+1)\cos k}{\cos k \cdot \cos(k+1)} - \frac{\cos(k+1)\sin k}{\cos k \cdot \cos(k+1)} \right)$ Simplify the terms: $T_k = \frac{1}{\sin 1} \left( \frac{\sin(k+1)}{\cos(k+1)} - \frac{\sin k}{\cos k} \right)$ Using the identity $\tan x = \frac{\sin x}{\cos x}$: $T_k = \frac{1}{\sin 1} (\tan(k+1) - \tan k)$

Now, we find the sum of the first $n$ terms, $S_n = \sum_{k=1}^{n} T_k$: $S_n = \sum_{k=1}^{n} \frac{1}{\sin 1} (\tan(k+1) - \tan k)$ $S_n = \frac{1}{\sin 1} \sum_{k=1}^{n} (\tan(k+1) - \tan k)$ This is a telescoping sum: For $k=1$: $\tan 2 - \tan 1$ For $k=2$: $\tan 3 - \tan 2$ For $k=3$: $\tan 4 - \tan 3$ ... For $k=n$: $\tan(n+1) - \tan n$

When we sum these terms, all intermediate terms cancel out: $S_n = \frac{1}{\sin 1} [(\tan 2 - \tan 1) + (\tan 3 - \tan 2) + (\tan 4 - \tan 3) + \dots + (\tan(n+1) - \tan n)]$ $S_n = \frac{1}{\sin 1} (\tan(n+1) - \tan 1)$

This is the sum of the first $n$ terms of the series. If the question implies an infinite series ($n \to \infty$), the term $\tan(n+1)$ does not converge as $n \to \infty$. The tangent function is periodic and its value oscillates between $-\infty$ and $+\infty$. Therefore, the infinite series diverges.

The angles (1, 2, 3, etc.) are assumed to be in radians, as no degree symbol is specified.

The final answer is $\boxed{\frac{\tan(n+1) - \tan 1}{\sin 1}}$

Explanation of the solution:

1. Identify General Term: The general term of the series is $T_k = \sec k \cdot \sec(k+1) = \frac{1}{\cos k \cdot \cos(k+1)}$.
2. Transform to Difference: Multiply and divide by $\sin((k+1)-k) = \sin 1$ to express $T_k$ as a difference of two terms. $T_k = \frac{1}{\sin 1} \cdot \frac{\sin((k+1)-k)}{\cos k \cdot \cos(k+1)} = \frac{1}{\sin 1} \left( \frac{\sin(k+1)\cos k - \cos(k+1)\sin k}{\cos k \cdot \cos(k+1)} \right)$.
3. Simplify to Tangent Form: Split the fraction and simplify using $\tan x = \frac{\sin x}{\cos x}$. $T_k = \frac{1}{\sin 1} \left( \frac{\sin(k+1)}{\cos(k+1)} - \frac{\sin k}{\cos k} \right) = \frac{1}{\sin 1} (\tan(k+1) - \tan k)$.
4. Telescoping Sum: Sum the terms from $k=1$ to $n$. All intermediate terms cancel out, leaving only the first and last terms. $S_n = \sum_{k=1}^{n} \frac{1}{\sin 1} (\tan(k+1) - \tan k) = \frac{1}{\sin 1} (\tan(n+1) - \tan 1)$.
5. Divergence: For an infinite series ($n \to \infty$), $\lim_{n \to \infty} \tan(n+1)$ does not exist, so the infinite series diverges. The provided answer is for the sum of the first 'n' terms.

Answer: The sum of the first $n$ terms of the series is $\frac{\tan(n+1) - \tan 1}{\sin 1}$.