Solveeit Logo
Login

Question

Question: Prove that $({}^{2n}C_0)^2 - ({}^{2n}C_1)^2 + ({}^{2n}C_2)^2 - \dots + ({}^{2n}C_{2n})^2 = (-1)^n {}...

Prove that (2nC0)2−(2nC1)2+(2nC2)2−⋯+(2nC2n)2=(−1)n2nCn({}^{2n}C_0)^2 - ({}^{2n}C_1)^2 + ({}^{2n}C_2)^2 - \dots + ({}^{2n}C_{2n})^2 = (-1)^n {}^{2n}C_n.

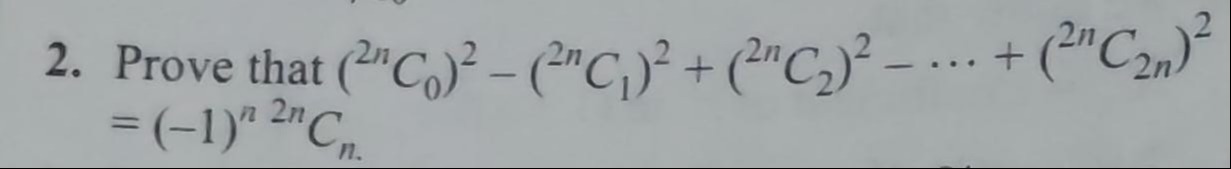
Answer

The identity to be proven is: (2nC0)2−(2nC1)2+(2nC2)2−⋯+(2nC2n)2=(−1)n2nCn({}^{2n}C_0)^2 - ({}^{2n}C_1)^2 + ({}^{2n}C_2)^2 - \dots + ({}^{2n}C_{2n})^2 = (-1)^n {}^{2n}C_n. Since this is a "Prove that" question, the answer is the proof itself.

Explanation

Solution

Let S=∑r=02n(−1)r(2nCr)2S = \sum_{r=0}^{2n} (-1)^r ({}^{2n}C_r)^2. Using 2nCr=2nC2n−r{}^{2n}C_r = {}^{2n}C_{2n-r}, we rewrite SS as ∑r=02n(−1)r(2nCr)(2nC2n−r)\sum_{r=0}^{2n} (-1)^r ({}^{2n}C_r) ({}^{2n}C_{2n-r}). This is the coefficient of x2nx^{2n} in the product (1−x)2n(1+x)2n=(1−x2)2n(1-x)^{2n} (1+x)^{2n} = (1-x^2)^{2n}. The expansion of (1−x2)2n(1-x^2)^{2n} is ∑k=02n(−1)k2nCkx2k\sum_{k=0}^{2n} (-1)^k {}^{2n}C_k x^{2k}. The coefficient of x2nx^{2n} occurs when 2k=2n2k=2n, so k=nk=n. The coefficient is (−1)n2nCn(-1)^n {}^{2n}C_n. Thus, S=(−1)n2nCnS = (-1)^n {}^{2n}C_n.