Question
Question: $\lim_{x \to 0^{+}} \sqrt{x} e^{\sin(\frac{1}{x})}$...
limx→0+xesin(x1)
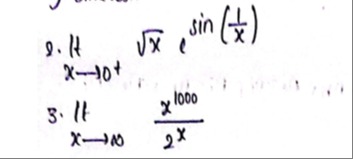
Answer
0
Explanation
Solution
The limit is evaluated by recognizing that one part of the product (x) tends to zero, while the other part (esin(1/x)) is bounded. Specifically, sin(1/x) oscillates between -1 and 1, so esin(1/x) oscillates between e−1 and e1. By the Squeeze Theorem, the product of a function tending to zero and a bounded function is zero.
