Question
Question: $\lim_{x \to 0} \frac{ln(1+x)-x}{x^2}$...
limx→0x2ln(1+x)−x
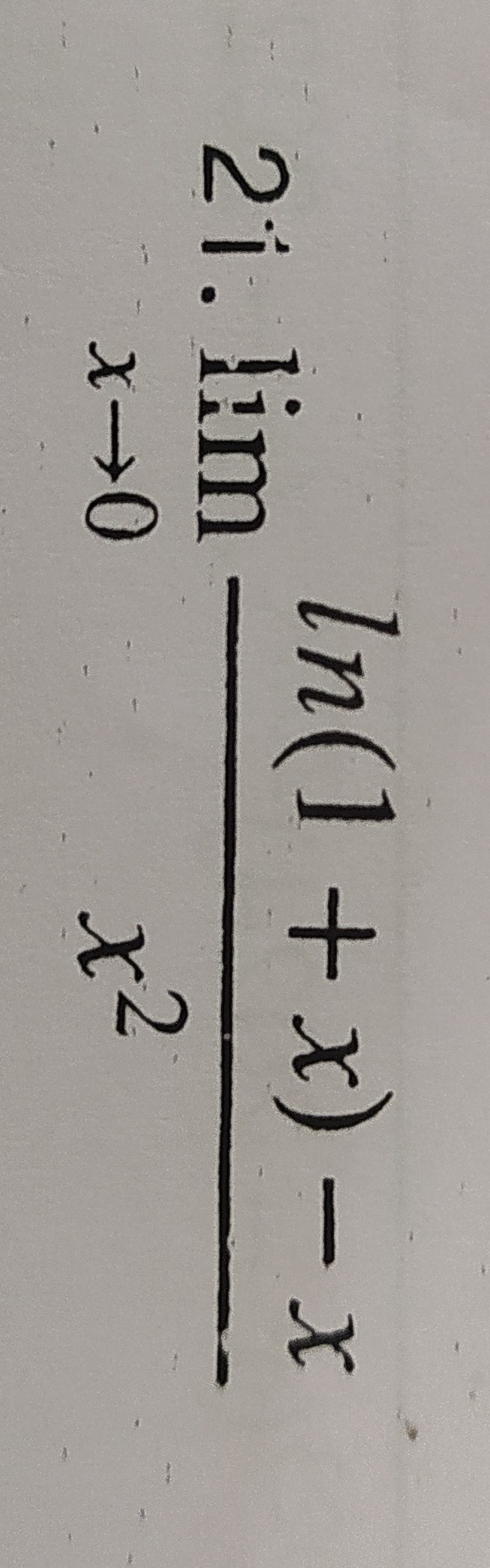
Answer
−21
Explanation
Solution
The limit is of the form 00 as x→0. Applying L'Hopital's Rule twice:
limx→0x2ln(1+x)−x=limx→02x1+x1−1=limx→02−(1+x)21=−21.
Alternatively, using the Taylor expansion ln(1+x)=x−2x2+O(x3), the expression becomes x2(x−2x2+O(x3))−x=x2−2x2+O(x3)=−21+O(x), which tends to −21 as x→0.
