Question
Question: Let $f(x) = \frac{e^{2x}-1-2x}{x^2}$. Find $\lim_{x\to 0} f(x)$....
Let f(x)=x2e2x−1−2x. Find limx→0f(x).
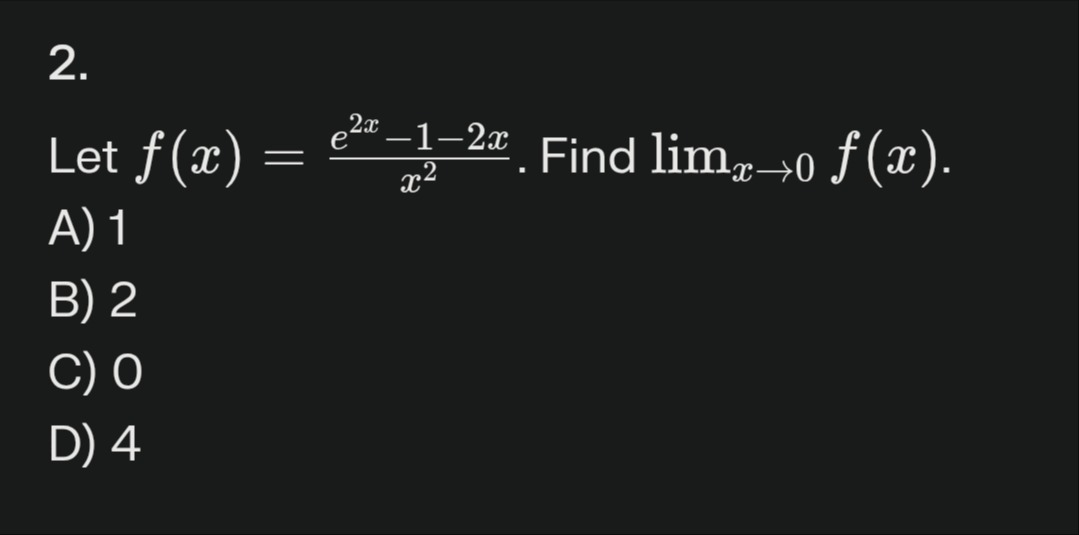
1
2
0
4
2
Solution
To find limx→0x2e2x−1−2x, we first check the form of the limit. Substituting x=0 gives 02e0−1−0=01−1=00, which is an indeterminate form.
We can use L'Hopital's Rule.
First application:
- Differentiate numerator: dxd(e2x−1−2x)=2e2x−2.
- Differentiate denominator: dxd(x2)=2x.
The limit becomes limx→02x2e2x−2. This is still 00 at x=0.
Second application of L'Hopital's Rule:
- Differentiate numerator: dxd(2e2x−2)=4e2x.
- Differentiate denominator: dxd(2x)=2.
The limit becomes limx→024e2x. Now, substitute x=0: 24e2(0)=24e0=24(1)=2.
Alternatively, using Taylor series expansion for e2x around x=0:
e2x=1+(2x)+2!(2x)2+3!(2x)3+⋯=1+2x+24x2+68x3+⋯=1+2x+2x2+34x3+…
Substitute this into the expression for f(x):
f(x)=x2(1+2x+2x2+34x3+…)−1−2x
f(x)=x22x2+34x3+…
Factor out x2 from the numerator:
f(x)=x2x2(2+34x+…)
Cancel x2 (since x=0 as x→0):
f(x)=2+34x+…
Now, take the limit as x→0:
limx→0f(x)=limx→0(2+34x+…)=2.
