Question
Question: Least value of $\frac{x^{2}y^{2}-2x^{2}y+2x^{2}+2xy-2x+1}{x^{2}y+x}$ is $\lambda$, then {where x,y $...
Least value of x2y+xx2y2−2x2y+2x2+2xy−2x+1 is λ, then {where x,y ∈ R+, x2y + x = 0}
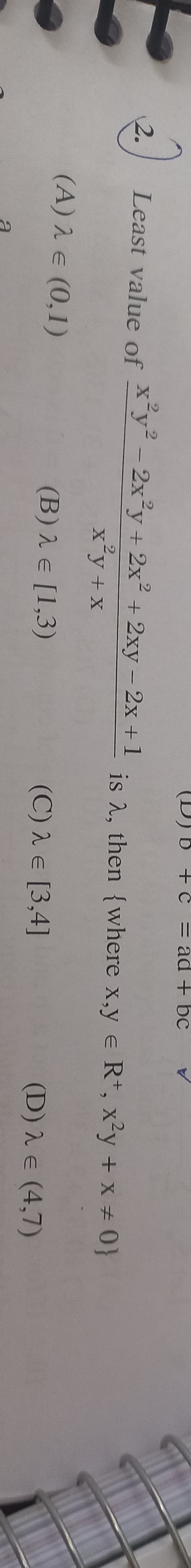
λ∈(0,1)
λ∈[1,3)
λ∈[3,4]
λ∈(4,7)
(A)
Solution
The given expression is E=x2y+xx2y2−2x2y+2x2+2xy−2x+1.
The numerator can be factored as: x2y2−2x2y+2x2+2xy−2x+1=(x2y2+2xy+1)−2x2y−2x+2x2=(xy+1)2−2x(xy+1)+2x2.
The denominator is x2y+x=x(xy+1).
So, the expression becomes: E=x(xy+1)(xy+1)2−2x(xy+1)+2x2=x(xy+1)(xy+1)2−x(xy+1)2x(xy+1)+x(xy+1)2x2=xxy+1−2+xy+12x
Let A=xxy+1. Since x,y∈R+, x>0 and y>0. Therefore, xy>0, so xy+1>1. Since x>0, A=xxy+1>0.
The expression E can be rewritten as: E=A−2+A2
To find the least value of E, we apply the AM-GM inequality to the positive terms A and A2: A+A2≥2A⋅A2=22
Substituting this back into the expression for E: E≥22−2.
The equality holds when A=A2, which means A2=2. Since A>0, A=2.
This value is achievable. For example, if x=1, then y+11=2, so y=2−1. Since 2≈1.414, y≈0.414>0. Thus, x=1,y=2−1 are valid positive real numbers.
The least value of the expression is λ=22−2. To determine the interval for λ: We know 2≈1.414. So, λ≈2×1.414−2=2.828−2=0.828. This value is greater than 0 and less than 1. Therefore, λ∈(0,1).
