Question

$L_1$ is a tangent drawn to the curve $x^2 - 4y^2 = 16$ at $A(5, \frac{3}{2})$. $L_2$ is another tangent parallel to $L_1$ which meets the curve at B. $L_3$ and $L_4$ are normals to the curve at A and B. Lines $L_1, L_2, L_3, L_4$ forms a rectangle, then which of the following is correct

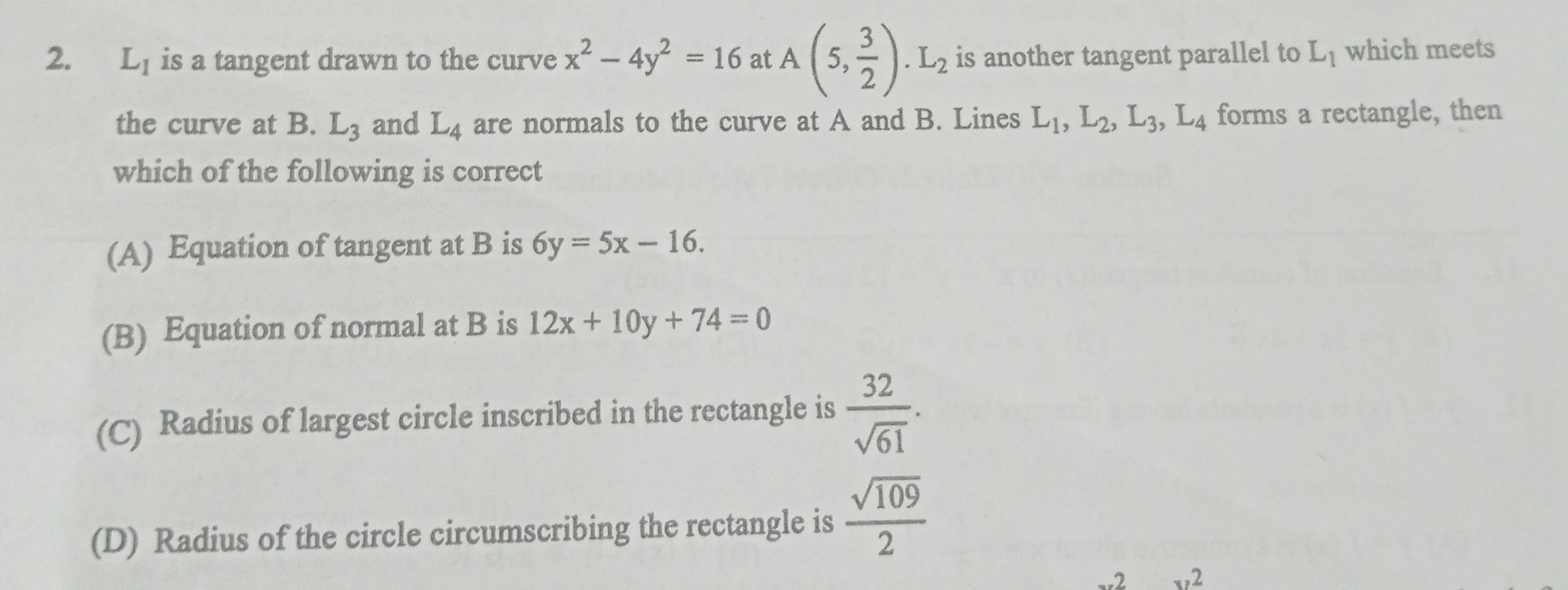
• A. Equation of tangent at B is $6y = 5x - 16$.
• B. Equation of normal at B is $12x + 10y + 74 = 0$
• C. Radius of largest circle inscribed in the rectangle is $\frac{32}{\sqrt{61}}$.
• D. Radius of the circle circumscribing the rectangle is $\frac{\sqrt{109}}{2}$

Answer 1

Answer: (D)

Radius of the circle circumscribing the rectangle is $\frac{\sqrt{109}}{2}

Answer 2

The given curve is a hyperbola $x^2 - 4y^2 = 16$, which can be written as $\frac{x^2}{16} - \frac{y^2}{4} = 1$. Here $a^2=16, b^2=4$. Point $A(5, \frac{3}{2})$ is on the curve since $5^2 - 4(\frac{3}{2})^2 = 25 - 4(\frac{9}{4}) = 25 - 9 = 16$.

$L_1$ is the tangent at $A(5, \frac{3}{2})$. The equation of the tangent at $(x_1, y_1)$ to $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ is $\frac{xx_1}{a^2} - \frac{yy_1}{b^2} = 1$. $L_1: \frac{x(5)}{16} - \frac{y(\frac{3}{2})}{4} = 1 \implies \frac{5x}{16} - \frac{3y}{8} = 1 \implies 5x - 6y = 16$. The slope of $L_1$ is $m_1 = \frac{5}{6}$.

$L_2$ is another tangent parallel to $L_1$. Its slope is $m_2 = m_1 = \frac{5}{6}$. The equation of tangent with slope $m$ is $y = mx \pm \sqrt{a^2m^2 - b^2}$. $y = \frac{5}{6}x \pm \sqrt{16(\frac{5}{6})^2 - 4} = \frac{5}{6}x \pm \sqrt{16(\frac{25}{36}) - 4} = \frac{5}{6}x \pm \sqrt{\frac{100}{9} - 4} = \frac{5}{6}x \pm \sqrt{\frac{64}{9}} = \frac{5}{6}x \pm \frac{8}{3}$. The two tangents are $y = \frac{5}{6}x + \frac{8}{3}$ ($6y = 5x + 16$ or $5x - 6y + 16 = 0$) and $y = \frac{5}{6}x - \frac{8}{3}$ ($6y = 5x - 16$ or $5x - 6y - 16 = 0$). $L_1$ is $5x - 6y - 16 = 0$. $L_2$ is $5x - 6y + 16 = 0$. $L_2$ meets the curve at B. The point of tangency $(x_1, y_1)$ for $y = mx + c$ is $(\frac{-a^2m}{c}, \frac{-b^2}{c})$. For $L_2: y = \frac{5}{6}x + \frac{8}{3}$, $m=\frac{5}{6}, c=\frac{8}{3}$. $x_B = \frac{-16(5/6)}{8/3} = \frac{-80/6}{8/3} = \frac{-80}{6} \times \frac{3}{8} = \frac{-10}{2} = -5$. $y_B = \frac{-4}{8/3} = \frac{-12}{8} = -\frac{3}{2}$. So $B = (-5, -\frac{3}{2})$.

$L_3$ and $L_4$ are normals at A and B. The slope of the normal is $-\frac{1}{m_{tangent}}$. Slope of $L_3$ (normal at A): $m_3 = -\frac{1}{m_1} = -\frac{6}{5}$. Equation of $L_3$: $y - \frac{3}{2} = -\frac{6}{5}(x - 5) \implies 10(y - \frac{3}{2}) = -12(x - 5) \implies 10y - 15 = -12x + 60 \implies 12x + 10y - 75 = 0$. Slope of $L_4$ (normal at B): $m_4 = -\frac{1}{m_2} = -\frac{6}{5}$. Equation of $L_4$: $y - (-\frac{3}{2}) = -\frac{6}{5}(x - (-5)) \implies y + \frac{3}{2} = -\frac{6}{5}(x + 5) \implies 10(y + \frac{3}{2}) = -12(x + 5) \implies 10y + 15 = -12x - 60 \implies 12x + 10y + 75 = 0$.

The four lines are $L_1: 5x - 6y - 16 = 0$, $L_2: 5x - 6y + 16 = 0$, $L_3: 12x + 10y - 75 = 0$, $L_4: 12x + 10y + 75 = 0$. $L_1 || L_2$ and $L_3 || L_4$. $m_1 m_3 = (\frac{5}{6})(-\frac{6}{5}) = -1$, so $L_1 \perp L_3$. The lines form a rectangle.

Let's check the options: (A) Equation of tangent at B is $6y = 5x - 16$. The tangent at B is $L_2: 5x - 6y + 16 = 0 \implies 6y = 5x + 16$. (A) is incorrect. (B) Equation of normal at B is $12x + 10y + 74 = 0$. The normal at B is $L_4: 12x + 10y + 75 = 0$. (B) is incorrect.

(C) Radius of largest circle inscribed in the rectangle. The side lengths of the rectangle are the distances between parallel lines. Distance between $L_1$ and $L_2$: $d_1 = \frac{|-16 - 16|}{\sqrt{5^2 + (-6)^2}} = \frac{32}{\sqrt{25 + 36}} = \frac{32}{\sqrt{61}}$. Distance between $L_3$ and $L_4$: $d_2 = \frac{|-75 - 75|}{\sqrt{12^2 + 10^2}} = \frac{150}{\sqrt{144 + 100}} = \frac{150}{2\sqrt{61}} = \frac{75}{\sqrt{61}}$. The diameter of the inscribed circle is $\min(d_1, d_2) = \min(\frac{32}{\sqrt{61}}, \frac{75}{\sqrt{61}}) = \frac{32}{\sqrt{61}}$. The radius is $\frac{1}{2} \times \frac{32}{\sqrt{61}} = \frac{16}{\sqrt{61}}$. (C) is incorrect.

(D) Radius of the circle circumscribing the rectangle. The diameter of the circumscribing circle is the length of the diagonal of the rectangle. The vertices A and B are opposite vertices of the rectangle. $A = (5, \frac{3}{2})$, $B = (-5, -\frac{3}{2})$. The distance AB is the length of the diagonal. $AB = \sqrt{(-5 - 5)^2 + (-\frac{3}{2} - \frac{3}{2})^2} = \sqrt{(-10)^2 + (-3)^2} = \sqrt{100 + 9} = \sqrt{109}$. The diameter of the circumscribing circle is $\sqrt{109}$. The radius is $\frac{\sqrt{109}}{2}$. (D) is correct.