Question

$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} f(x) dx =$

Where $f(x) = \sin|x| + \cos|x|, x \in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$.

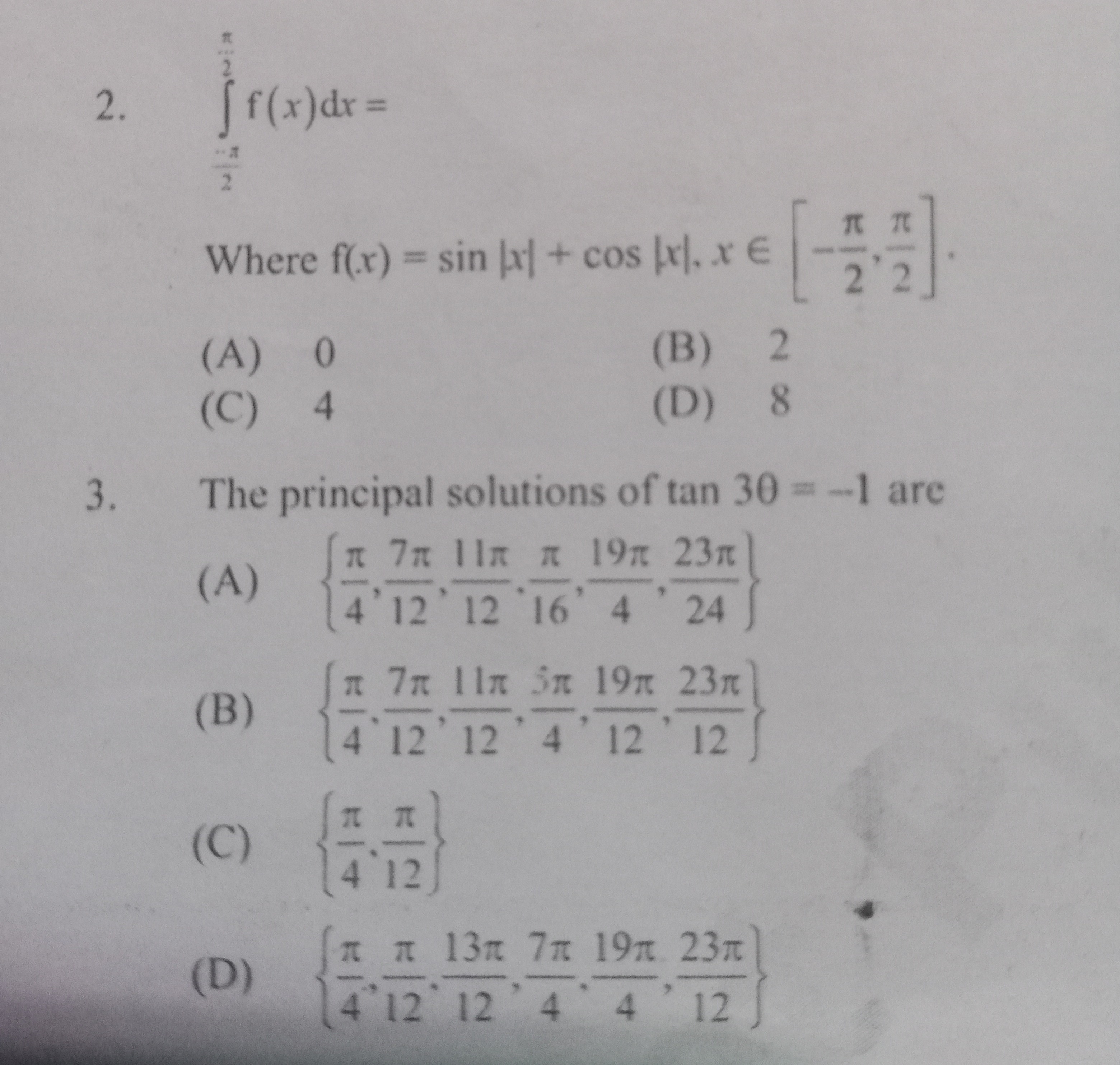
• A. 0
• B. 2
• C. 4
• D. 8

Answer 1

Answer: (C)

4

Answer 2

To evaluate the definite integral $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} f(x) dx$, where $f(x) = \sin|x| + \cos|x|$, we note that the interval of integration is symmetric about 0. Also, $f(x)$ is an even function because $f(-x) = \sin|-x| + \cos|-x| = \sin|x| + \cos|x| = f(x)$.

For an even function, $\int_{-a}^{a} f(x) dx = 2 \int_{0}^{a} f(x) dx$. Therefore,

$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\sin|x| + \cos|x|) dx = 2 \int_{0}^{\frac{\pi}{2}} (\sin x + \cos x) dx$

Since $|x| = x$ for $x \in [0, \frac{\pi}{2}]$.

Now, we evaluate the integral:

$2 \int_{0}^{\frac{\pi}{2}} (\sin x + \cos x) dx = 2 [-\cos x + \sin x]_{0}^{\frac{\pi}{2}} = 2 [ (-\cos(\frac{\pi}{2}) + \sin(\frac{\pi}{2})) - (-\cos(0) + \sin(0)) ] = 2 [ (0 + 1) - (-1 + 0) ] = 2 [1 + 1] = 4$.

Thus, the value of the integral is 4.