Question

$\int(3x^2+2x+3)dx =$

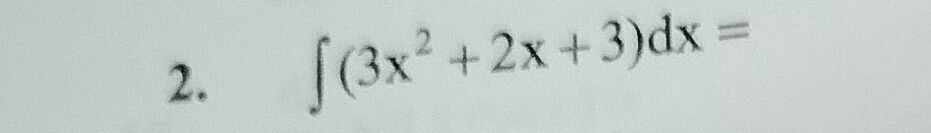
Answer 1

$x^3 + x^2 + 3x + C$

Answer 2

The integral of the polynomial $3x^2+2x+3$ is found by integrating each term separately using the power rule $\int x^n dx = \frac{x^{n+1}}{n+1}$ and the constant multiple rule $\int c f(x) dx = c \int f(x) dx$. The integral of $3x^2$ is $3 \cdot \frac{x^3}{3} = x^3$. The integral of $2x$ is $2 \cdot \frac{x^2}{2} = x^2$. The integral of the constant $3$ is $3x$. Combining these results and adding the constant of integration $C$ gives the final answer.