Question

$\int (1+2x+3x^2+4x^3+...)dx,(0<|x|<1)$

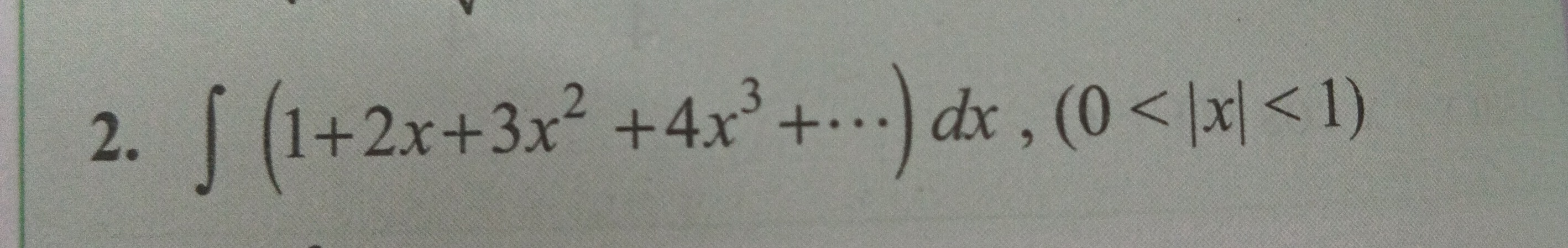
Answer 1

$\frac{1}{1-x}+C$

Answer 2

The given series $1+2x+3x^2+4x^3+...$ is the derivative of the geometric series $1+x+x^2+x^3+... = \frac{1}{1-x}$.

Thus, the series can be written as $\frac{d}{dx}\left(\frac{1}{1-x}\right) = \frac{1}{(1-x)^2}$.

The integral becomes $\int \frac{1}{(1-x)^2} dx$.

Using substitution $u=1-x$, $du=-dx$, the integral transforms to $-\int u^{-2} du$.

This evaluates to $-(-u^{-1}) + C = \frac{1}{u} + C$.

Substituting back $u=1-x$, the result is $\frac{1}{1-x} + C$.