Question

$\int (1 - \cos x) \csc^2 x \, dx$

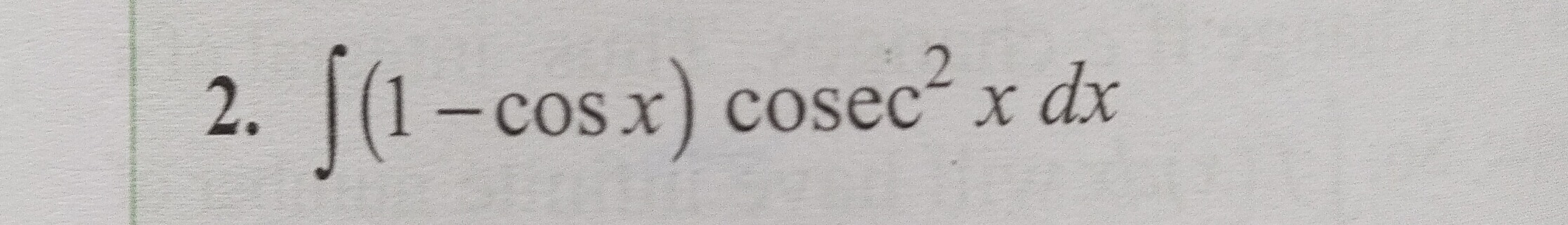
Answer 1

$\tan \frac{x}{2} + C$

Answer 2

The integral $\int (1 - \cos x) \csc^2 x \, dx$ is solved by first rewriting $\csc^2 x$ as $\frac{1}{\sin^2 x}$. Then, $\sin^2 x$ is replaced by $1 - \cos^2 x$, which factors as $(1 - \cos x)(1 + \cos x)$. Cancelling the $(1 - \cos x)$ term simplifies the integrand to $\frac{1}{1 + \cos x}$. Using the half-angle identity $1 + \cos x = 2\cos^2 \frac{x}{2}$, the integrand becomes $\frac{1}{2\cos^2 \frac{x}{2}} = \frac{1}{2}\sec^2 \frac{x}{2}$. Finally, integrating $\frac{1}{2}\sec^2 \frac{x}{2}$ with respect to $x$ yields $\tan \frac{x}{2} + C$.