Question
Question: In the given circuit the current flowing through the resistance 20 $\Omega$ is 0.3 A, while the amme...
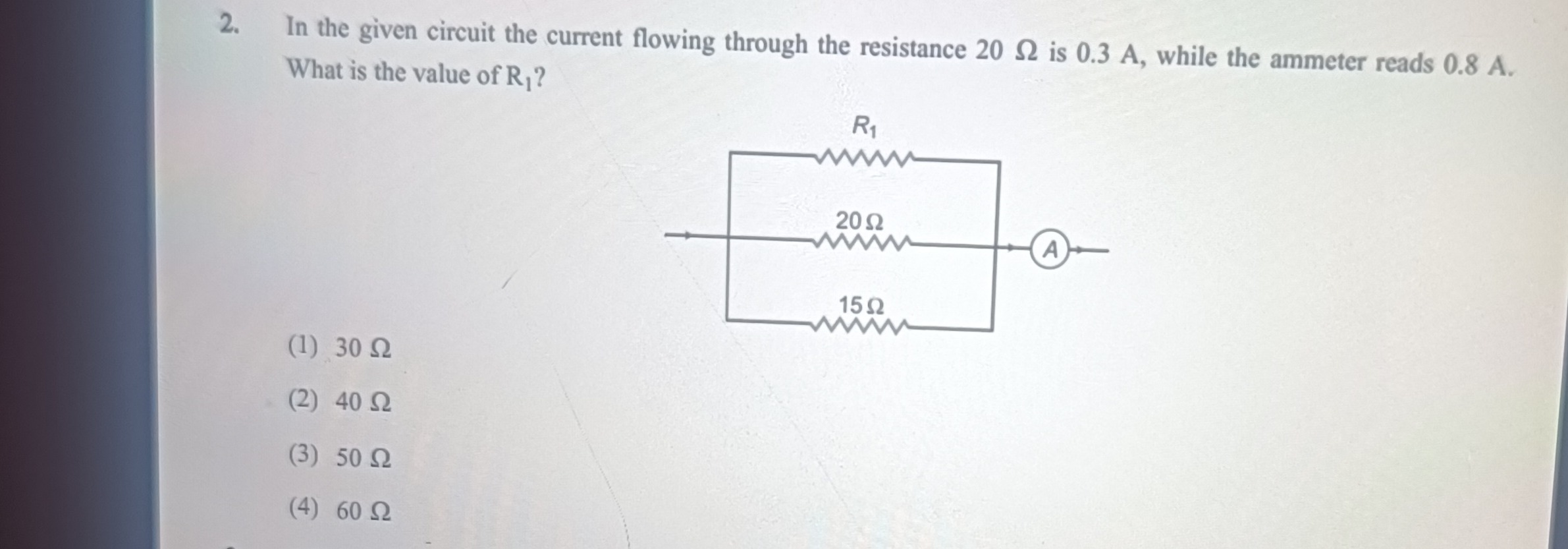
In the given circuit the current flowing through the resistance 20 Ω is 0.3 A, while the ammeter reads 0.8 A. What is the value of R₁?
30 Ω
40 Ω
50 Ω
60 Ω
60 Ω
Solution
The circuit shows three resistors (R₁, 20 Ω, and 15 Ω) connected in parallel. In a parallel circuit, the voltage across each branch is the same. The total current entering the parallel combination is the sum of the currents in each branch (Kirchhoff's Current Law).
Given:
- Current through 20 Ω resistor (I20) = 0.3 A
- Total current (Itotal) = 0.8 A
Step 1: Calculate the voltage across the 20 Ω resistor. Using Ohm's Law, V=I×R: Voltage across 20 Ω resistor (V) = I20×20Ω
V=0.3A×20Ω
V=6V
Step 2: Determine the voltage across all parallel branches. Since the resistors are in parallel, the voltage across R₁, the 20 Ω resistor, and the 15 Ω resistor is the same, which is 6 V.
Step 3: Calculate the current through the 15 Ω resistor. Using Ohm's Law, I=V/R: Current through 15 Ω resistor (I15) = V/15Ω
I15=6V/15Ω
I15=0.4A
Step 4: Calculate the current through R₁. According to Kirchhoff's Current Law, the total current is the sum of currents in the parallel branches:
Itotal=IR1+I20+I15
0.8A=IR1+0.3A+0.4A
0.8A=IR1+0.7A
IR1=0.8A−0.7A
IR1=0.1A
Step 5: Calculate the value of R₁. Using Ohm's Law, R=V/I:
R1=V/IR1
R1=6V/0.1A
R1=60Ω
The value of R₁ is 60 Ω.
