Question

In the expansion of $\left[\frac{1}{a}+a^{\log_{10}a}\right]^5$, if the value of the third term is 1000, then the value of $a$ is

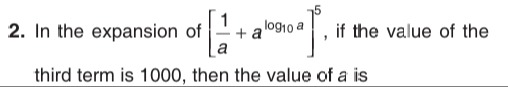
Answer 1

a = 100 or a = 1/sqrt(10)

Answer 2

The general term in the binomial expansion of $(x+y)^n$ is given by $T_{r+1} = \binom{n}{r} x^{n-r} y^r$.

In this case, $x = \frac{1}{a}$, $y = a^{\log_{10}a}$, and $n = 5$. We are looking for the third term, so $r = 2$.

$T_3 = \binom{5}{2} \left(\frac{1}{a}\right)^{5-2} \left(a^{\log_{10}a}\right)^2 = 10 \cdot a^{-3} \cdot a^{2\log_{10}a} = 10 \cdot a^{2\log_{10}a - 3}$.

Given that $T_3 = 1000$, we have:

$10 \cdot a^{2\log_{10}a - 3} = 1000$

$a^{2\log_{10}a - 3} = 100$

Taking $\log_{10}$ of both sides:

$(2\log_{10}a - 3) \log_{10}a = \log_{10}100 = 2$

Let $t = \log_{10}a$, then:

$(2t - 3)t = 2$

$2t^2 - 3t - 2 = 0$

$(2t + 1)(t - 2) = 0$

So, $t = -\frac{1}{2}$ or $t = 2$.

If $t = -\frac{1}{2}$, then $\log_{10}a = -\frac{1}{2}$, so $a = 10^{-1/2} = \frac{1}{\sqrt{10}}$.

If $t = 2$, then $\log_{10}a = 2$, so $a = 10^2 = 100$.

Therefore, the possible values for $a$ are $100$ and $\frac{1}{\sqrt{10}}$.