Question
Question: In a Young's double slit experiment, a plane monochromatic wave of wavelength 6000 Å, is incident no...
In a Young's double slit experiment, a plane monochromatic wave of wavelength 6000 Å, is incident normally on the slit plane as shown in the figure. A perfectly transparent film of thickness t, and refractive index 1.5 is placed in front of the slit S₁. The intensity of light on the screen near O is
I due to each slit.
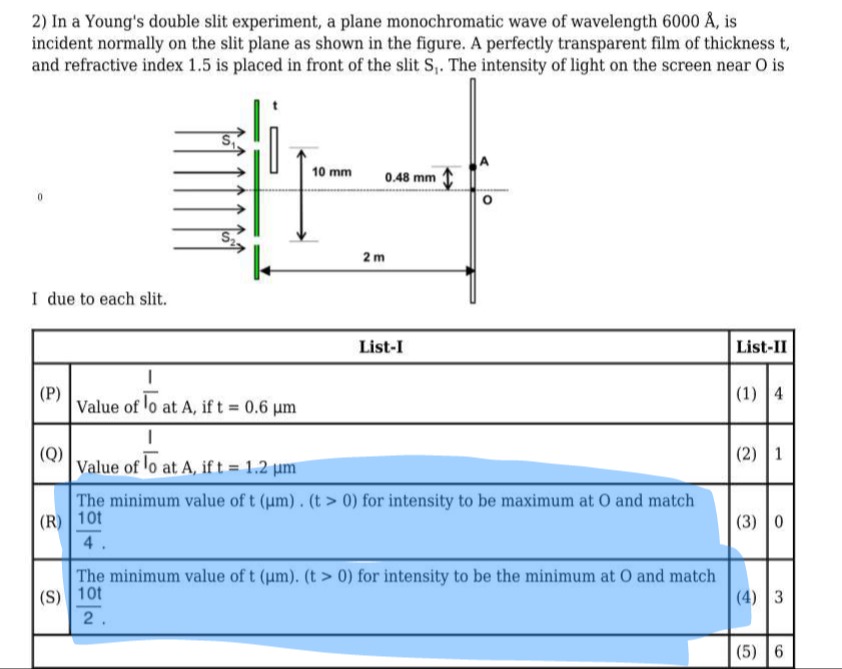
Value of I0I at A, if t = 0.6 µm
Value of I0I at A, if t = 1.2 µm
The minimum value of t (µm). (t > 0) for intensity to be maximum at O and match 410t.
The minimum value of t (µm). (t > 0) for intensity to be the minimum at O and match 210t.
4
1
0
3
6
P-3, Q-1, R-4, S-4
Solution
The intensity at a point on the screen in a Young's double-slit experiment is given by I=4I0cos2(2ϕ), where I0 is the intensity due to each slit and ϕ is the phase difference between the waves from the two slits at that point.
The phase difference is given by ϕ=λ2πΔx, where Δx is the path difference.
In the presence of a film of thickness t and refractive index μ in front of slit S₁, the additional path difference introduced is (μ−1)t.
The distance between the slits is d=10 mm=10×10−3 m. The distance between the slits and the screen is D=2 m. The wavelength of light is λ=6000 A˚=6000×10−10 m=6×10−7 m=0.6 µm. The refractive index of the film is μ=1.5. The additional path difference due to the film is (μ−1)t=(1.5−1)t=0.5t.
Let A be a point on the screen at a distance yA=0.48 mm=0.48×10−3 m from the central point O. The path difference at A without the film is Δxair=DyAd=2(0.48×10−3)(10×10−3)=2.4×10−6 m. In terms of wavelength, Δxair=6×10−72.4×10−6λ=4λ. The total path difference at A with the film in front of S₁ is ΔxA=Δxair−(μ−1)t=4λ−0.5t. The phase difference at A is ϕA=λ2πΔxA=λ2π(4λ−0.5t)=8π−λπt. The intensity at A is IA=4I0cos2(2ϕA)=4I0cos2(28π−λπt)=4I0cos2(4π−2λπt)=4I0cos2(2λπt).
(P) Value of I0IA at A, if t=0.6 µm. I0IA=4cos2(2λπt). Given t=0.6 µm and λ=0.6 µm. 2λπt=2(0.6 µm)π(0.6 µm)=2π. I0IA=4cos2(2π)=4×02=0. (P) matches with (3).
(Q) Value of I0IA at A, if t=1.2 µm. Given t=1.2 µm and λ=0.6 µm. 2λπt=2(0.6 µm)π(1.2 µm)=1.21.2π=π. I0IA=4cos2(π)=4×(−1)2=4. (Q) matches with (1).
(R) The minimum value of t (µm), (t>0) for intensity to be maximum at O. At point O, yO=0. The path difference at O without the film is 0. The total path difference at O with the film is ΔxO=0−(μ−1)t=−0.5t. The phase difference at O is ϕO=λ2π(−0.5t)=−λπt. The intensity at O is IO=4I0cos2(2ϕO)=4I0cos2(−2λπt)=4I0cos2(2λπt). For maximum intensity at O, cos2(2λπt)=1. This occurs when 2λπt=nπ, where n is an integer. t=2nλ. For minimum t>0, we take n=1. tmin=2λ=2×0.6 µm=1.2 µm. We need to match 410t. 410tmin=410×1.2=412=3. (R) matches with (4).
(S) The minimum value of t (µm), (t>0) for intensity to be minimum at O. For minimum intensity at O, cos2(2λπt)=0. This occurs when 2λπt=(n+21)π, where n is an integer. t=(2n+1)λ. For minimum t>0, we take n=0. tmin=(2(0)+1)λ=λ=0.6 µm. We need to match 210t. 210tmin=210×0.6=26=3. (S) matches with (4).
Matches: (P) -> (3) (Q) -> (1) (R) -> (4) (S) -> (4)
Final Answer should be a mapping from List-I to List-II. P-3, Q-1, R-4, S-4.
