Question
Question: If the value of $\cos\frac{2\pi}{7} + \cos\frac{4\pi}{7} + \cos\frac{6\pi}{7} + \cos\frac{7\pi}{7} =...
If the value of cos72π+cos74π+cos76π+cos77π=2l. Find the value of l.
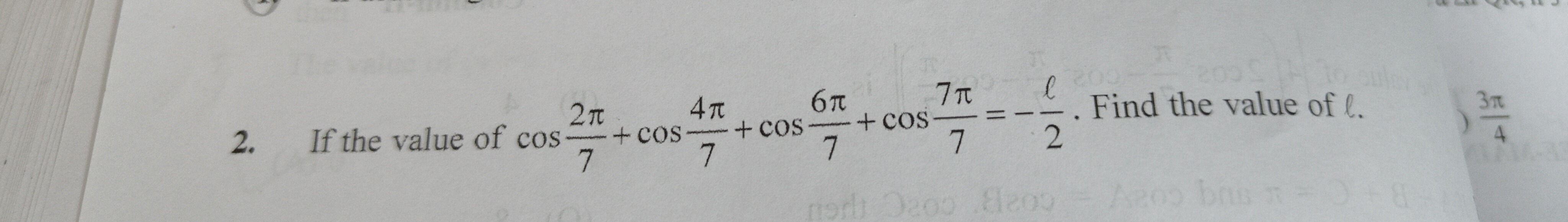
-3
Solution
The problem asks for the value of l given the equation:
cos(2π/7) + cos(4π/7) + cos(6π/7) + cos(7π/7) = l/2.
First, let's evaluate the last term:
cos(7π/7) = cos(π) = -1.
Now, consider the sum of the first three terms: S' = cos(2π/7) + cos(4π/7) + cos(6π/7).
This sum can be evaluated using the properties of roots of unity.
Consider the equation z^7 - 1 = 0. The roots are z_k = e^(i2kπ/7) for k = 0, 1, ..., 6.
The sum of these roots is zero:
Σ_(k=0)^6 z_k = 0
e^(i0) + e^(i2π/7) + e^(i4π/7) + e^(i6π/7) + e^(i8π/7) + e^(i10π/7) + e^(i12π/7) = 0.
Using Euler's formula e^(ix) = cos(x) + i sin(x), and taking the real part of the sum:
1 + cos(2π/7) + cos(4π/7) + cos(6π/7) + cos(8π/7) + cos(10π/7) + cos(12π/7) = 0.
We use the property cos(2π - x) = cos(x) and cos(π + x) = -cos(x):
cos(8π/7) = cos(π + π/7) = -cos(π/7)
cos(10π/7) = cos(π + 3π/7) = -cos(3π/7)
cos(12π/7) = cos(2π - 2π/7) = cos(2π/7)
However, a simpler symmetry can be used: cos(2(n-k)π/n) = cos(2kπ/n).
For n=7:
cos(12π/7) = cos(2π(6/7)) = cos(2π(1-1/7)) = cos(2π/7).
cos(10π/7) = cos(2π(5/7)) = cos(2π(1-2/7)) = cos(4π/7).
cos(8π/7) = cos(2π(4/7)) = cos(2π(1-3/7)) = cos(6π/7).
Substituting these into the sum of cosines:
1 + cos(2π/7) + cos(4π/7) + cos(6π/7) + cos(6π/7) + cos(4π/7) + cos(2π/7) = 0.
1 + 2[cos(2π/7) + cos(4π/7) + cos(6π/7)] = 0.
2[cos(2π/7) + cos(4π/7) + cos(6π/7)] = -1.
cos(2π/7) + cos(4π/7) + cos(6π/7) = -1/2.
This matches the result from the similar question.
Now, substitute this value back into the original equation:
(-1/2) + cos(7π/7) = l/2.
(-1/2) + (-1) = l/2.
-1/2 - 2/2 = l/2.
-3/2 = l/2.
Therefore, l = -3.
