Question

If $\sin \alpha$ & $\cos \alpha$ are the roots of the equation $ax^2 + bx + c = 0$ then

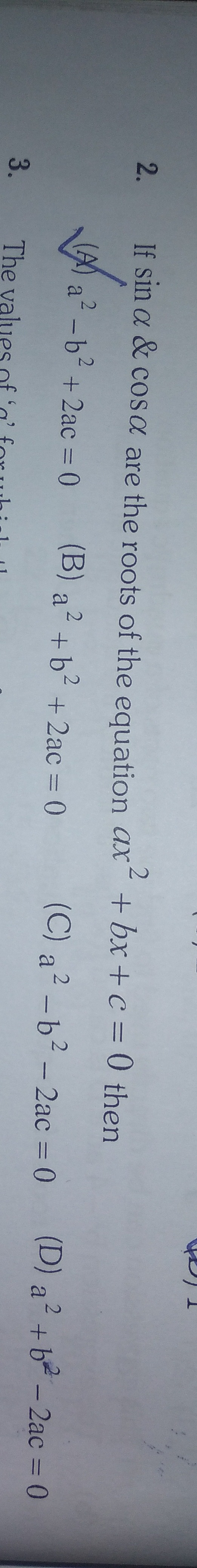
• A. a^2 - b^2 + 2ac = 0
• B. a^2 + b^2 + 2ac = 0
• C. a^2 - b^2 - 2ac = 0
• D. a^2 + b^2 - 2ac = 0

Answer 1

Answer: (A)

a^2 - b^2 + 2ac = 0

Answer 2

Given roots are $\sin \alpha$ and $\cos \alpha$ for $ax^2 + bx + c = 0$. Using Vieta's formulas: $\sin \alpha + \cos \alpha = -b/a$, $\sin \alpha \cos \alpha = c/a$. Square the sum: $(\sin \alpha + \cos \alpha)^2 = (-b/a)^2$. Use identity $(\sin \alpha + \cos \alpha)^2 = 1 + 2 \sin \alpha \cos \alpha$. Substitute: $1 + 2(c/a) = b^2/a^2$. Multiply by $a^2$ and rearrange: $a^2 + 2ac = b^2 \implies a^2 - b^2 + 2ac = 0$.