Question

If $P(B)=\frac{4}{3}$, $P(\overline{A}\cap B\cap \overline{C})=\frac{1}{3}$ and $P(\overline{A}\cap B\cap C)=\frac{1}{3}$, then $P(B\cap C)$ is

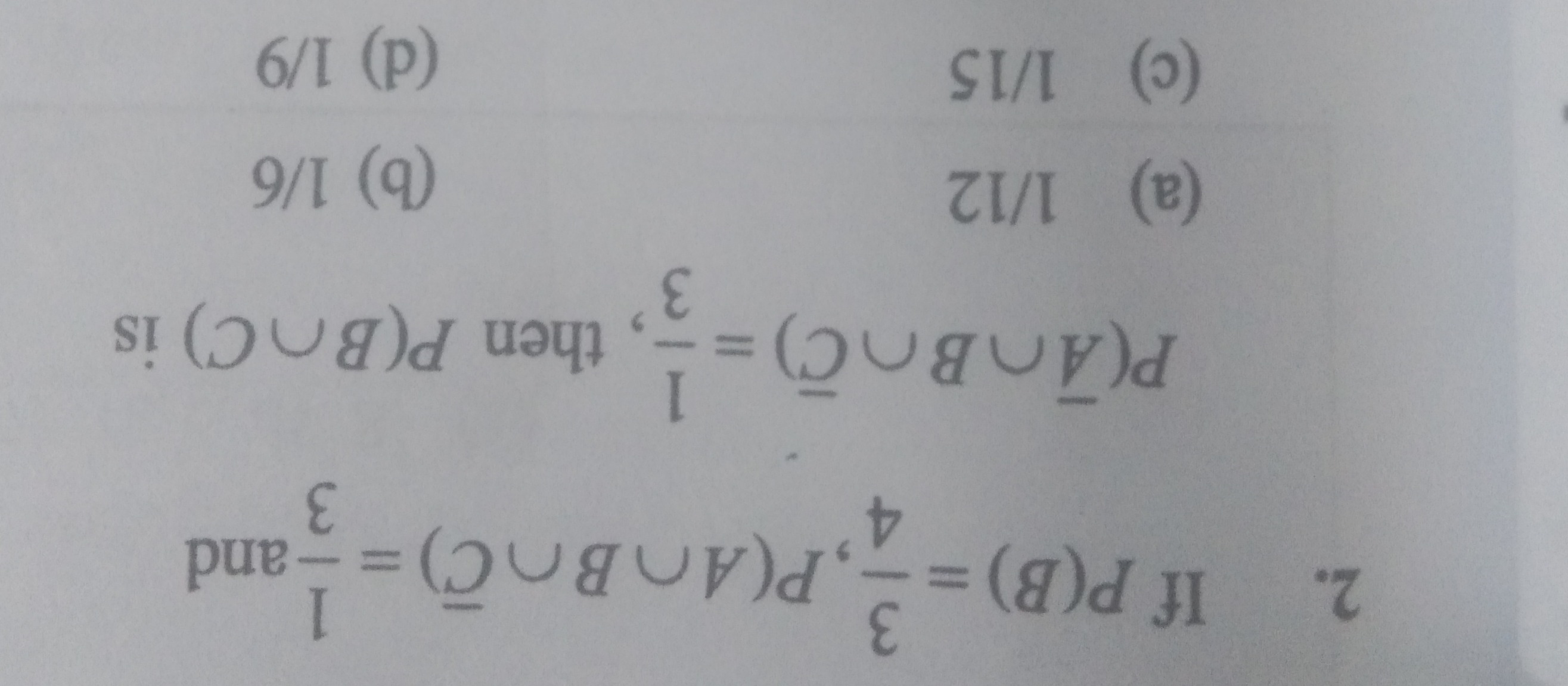
• A. 1/12
• B. 1/6
• C. 1/15
• D. 1/9

Answer 1

1/12

Answer 2

The event $B$ can be partitioned into disjoint events $B \cap C$ and $B \cap \overline{C}$. So, $P(B) = P(B \cap C) + P(B \cap \overline{C})$.

The event $B \cap \overline{C}$ can be partitioned into disjoint events $A \cap B \cap \overline{C}$ and $\overline{A} \cap B \cap \overline{C}$. So, $P(B \cap \overline{C}) = P(A \cap B \cap \overline{C}) + P(\overline{A} \cap B \cap \overline{C})$.

Combining these, $P(B) = P(B \cap C) + P(A \cap B \cap \overline{C}) + P(\overline{A} \cap B \cap \overline{C})$.

Rearranging to find $P(B \cap C)$: $P(B \cap C) = P(B) - P(A \cap B \cap \overline{C}) - P(\overline{A} \cap B \cap \overline{C})$.

The given question has $P(B)=\frac{4}{3}$, $P(\overline{A}\cap B\cap \overline{C})=\frac{1}{3}$ and $P(\overline{A}\cap B\cap C)=\frac{1}{3}$. The value $P(B)=\frac{4}{3}$ is inconsistent. Assuming the question intended to be solvable and similar to the similar question, we use the values from the similar question: $P(B)=\frac{3}{4}$, $P(A\cap B\cap \overline{C})=\frac{1}{3}$ and $P(\overline{A}\cap B\cap \overline{C})=\frac{1}{3}$.

Using the formula: $P(B \cap C) = \frac{3}{4} - \frac{1}{3} - \frac{1}{3} = \frac{3}{4} - \frac{2}{3} = \frac{9-8}{12} = \frac{1}{12}$.

The final answer is $\frac{1}{12}$.