Question

If $f(x)=\prod_{i=1}^{3}(x-a_i)+\sum_{i=1}^{3}a_i-3x$ where $a_i < a_{i+1}$ for i = 1, 2, then f(x) = 0 has :

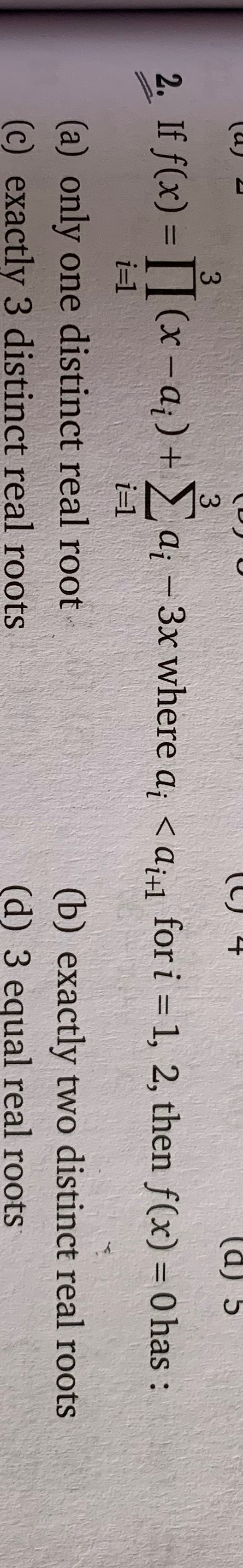
• A. only one distinct real root
• B. exactly two distinct real roots
• C. exactly 3 distinct real roots
• D. 3 equal real roots

Answer 1

Answer: (C)

exactly 3 distinct real roots

Answer 2

Let the given function be $f(x)=\prod_{i=1}^{3}(x-a_i)+\sum_{i=1}^{3}a_i-3x$, where $a_1 < a_2 < a_3$. This can be written as $f(x) = (x-a_1)(x-a_2)(x-a_3) + (a_1+a_2+a_3) - 3x$.

$f(x)$ is a cubic polynomial in $x$. As $x \to \infty$, $f(x) \to \infty$, and as $x \to -\infty$, $f(x) \to -\infty$. A cubic polynomial with real coefficients must have at least one real root.

Let's evaluate the function at the points $a_1, a_2, a_3$:

$f(a_1) = (a_1-a_1)(a_1-a_2)(a_1-a_3) + (a_1+a_2+a_3) - 3a_1 = 0 + a_1+a_2+a_3 - 3a_1 = a_2+a_3-2a_1$. Since $a_1 < a_2$ and $a_1 < a_3$, we have $a_2-a_1 > 0$ and $a_3-a_1 > 0$. $f(a_1) = (a_2-a_1) + (a_3-a_1) > 0$.

$f(a_2) = (a_2-a_1)(a_2-a_2)(a_2-a_3) + (a_1+a_2+a_3) - 3a_2 = 0 + a_1+a_2+a_3 - 3a_2 = a_1+a_3-2a_2$. $f(a_2) = (a_1-a_2) + (a_3-a_2)$. Since $a_1 < a_2 < a_3$, $a_1-a_2 < 0$ and $a_3-a_2 > 0$. The sign of $f(a_2)$ depends on the relative magnitudes of $|a_1-a_2|$ and $|a_3-a_2|$. $f(a_2)$ can be positive, negative, or zero.

$f(a_3) = (a_3-a_1)(a_3-a_2)(a_3-a_3) + (a_1+a_2+a_3) - 3a_3 = 0 + a_1+a_2+a_3 - 3a_3 = a_1+a_2-2a_3$. Since $a_1 < a_3$ and $a_2 < a_3$, we have $a_1-a_3 < 0$ and $a_2-a_3 < 0$. $f(a_3) = (a_1-a_3) + (a_2-a_3) < 0$.

We have $f(a_1) > 0$ and $f(a_3) < 0$. Since $f(x)$ is continuous and $a_1 < a_3$, by the Intermediate Value Theorem, there must be at least one real root in the interval $(a_1, a_3)$.

To determine the exact number of distinct real roots, let's consider the derivative of $f(x)$. $f'(x) = \frac{d}{dx}[(x-a_1)(x-a_2)(x-a_3)] + \frac{d}{dx}[a_1+a_2+a_3-3x]$ $f'(x) = (x-a_2)(x-a_3) + (x-a_1)(x-a_3) + (x-a_1)(x-a_2) - 3$. This is a quadratic function of $x$.

$f'(x) = (x^2 - (a_2+a_3)x + a_2a_3) + (x^2 - (a_1+a_3)x + a_1a_3) + (x^2 - (a_1+a_2)x + a_1a_2) - 3$ $f'(x) = 3x^2 - 2(a_1+a_2+a_3)x + (a_1a_2 + a_1a_3 + a_2a_3 - 3)$. The discriminant of this quadratic is $\Delta' = (-2(a_1+a_2+a_3))^2 - 4(3)(a_1a_2 + a_1a_3 + a_2a_3 - 3)$ $\Delta' = 4(a_1+a_2+a_3)^2 - 12(a_1a_2 + a_1a_3 + a_2a_3) + 36$ $\Delta' = 4(a_1^2+a_2^2+a_3^2 + 2a_1a_2 + 2a_1a_3 + 2a_2a_3) - 12(a_1a_2 + a_1a_3 + a_2a_3) + 36$ $\Delta' = 4(a_1^2+a_2^2+a_3^2) + 8(a_1a_2 + a_1a_3 + a_2a_3) - 12(a_1a_2 + a_1a_3 + a_2a_3) + 36$ $\Delta' = 4(a_1^2+a_2^2+a_3^2) - 4(a_1a_2 + a_1a_3 + a_2a_3) + 36$ $\Delta' = 2(2a_1^2+2a_2^2+2a_3^2 - 2a_1a_2 - 2a_1a_3 - 2a_2a_3) + 36$ $\Delta' = 2((a_1-a_2)^2 + (a_1-a_3)^2 + (a_2-a_3)^2) + 36$. Since $a_1 < a_2 < a_3$, the terms $(a_1-a_2)^2$, $(a_1-a_3)^2$, and $(a_2-a_3)^2$ are all positive. Thus, $\Delta' > 0$. This means $f'(x) = 0$ has two distinct real roots, say $r_1$ and $r_2$, with $r_1 < r_2$. These are the critical points of $f(x)$.

A cubic function with two distinct real critical points has a local maximum at one critical point and a local minimum at the other. For the equation $f(x)=0$ to have three distinct real roots, the local maximum must be positive and the local minimum must be negative.

We know $f(a_1) > 0$ and $f(a_3) < 0$.

Case 1: $f(a_2) > 0$. We have signs $+ \quad + \quad -$. $f(x) \to -\infty$ as $x \to -\infty$. $f(a_1) > 0$. There is a root in $(-\infty, a_1)$. $f(a_1) > 0$, $f(a_2) > 0$. No guaranteed root in $(a_1, a_2)$. $f(a_2) > 0$, $f(a_3) < 0$. There is a root in $(a_2, a_3)$. $f(a_3) < 0$. $f(x) \to \infty$ as $x \to \infty$. No guaranteed root in $(a_3, \infty)$. However, a cubic polynomial must have 1 or 3 real roots (counting multiplicity). Since we found roots in $(-\infty, a_1)$ and $(a_2, a_3)$, there must be a third real root. This third root must be in $(a_3, \infty)$ because $f(a_3) < 0$ and $f(x) \to \infty$. So in this case, there are three real roots: one in $(-\infty, a_1)$, one in $(a_2, a_3)$, and one in $(a_3, \infty)$. Are they distinct? Yes, because they are in disjoint intervals.

Case 2: $f(a_2) < 0$. We have signs $+ \quad - \quad -$. $f(x) \to -\infty$ as $x \to -\infty$. $f(a_1) > 0$. There is a root in $(-\infty, a_1)$. $f(a_1) > 0$, $f(a_2) < 0$. There is a root in $(a_1, a_2)$. $f(a_2) < 0$, $f(a_3) < 0$. No guaranteed root in $(a_2, a_3)$. $f(a_3) < 0$. $f(x) \to \infty$ as $x \to \infty$. There is a root in $(a_3, \infty)$. So in this case, there are three real roots: one in $(-\infty, a_1)$, one in $(a_1, a_2)$, and one in $(a_3, \infty)$. Are they distinct? Yes, because they are in disjoint intervals.

Case 3: $f(a_2) = 0$. We have signs $+ \quad 0 \quad -$. $a_2$ is a root. $f(x) \to -\infty$ as $x \to -\infty$. $f(a_1) > 0$. There is a root in $(-\infty, a_1)$. $f(a_1) > 0$, $f(a_2) = 0$. $a_2$ is a root. $f(a_2) = 0$, $f(a_3) < 0$. $a_2$ is a root. $f(a_3) < 0$. $f(x) \to \infty$ as $x \to \infty$. There is a root in $(a_3, \infty)$. So we have a root in $(-\infty, a_1)$, the root $a_2$, and a root in $(a_3, \infty)$. These are three distinct real roots.

In all possible cases for the sign of $f(a_2)$, we find that there are three distinct real roots.

Therefore, the final answer is exactly 3 distinct real roots.