Question

If $f: [2, \infty) \to [8, \infty)$ is a surjective function defined by $f(x) = x^2 - (p-2)x + 3p - 2$, $p \in \mathbb{R}$ then sum of values of $p$ is $m + \sqrt{n}$, where $m, n \in \mathbb{N}$. Find the value of $\frac{n}{m}$.

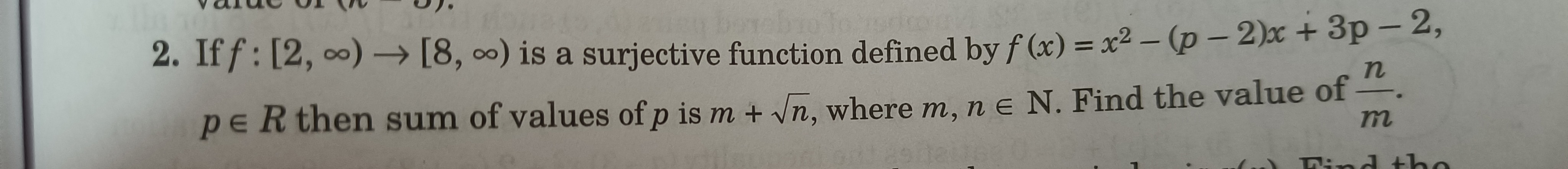
• A. 2
• B. 3
• C. 4
• D. 5

Answer 1

Answer: (A)

2

Answer 2

The function $f(x) = x^2 - (p-2)x + 3p - 2$ is a quadratic with domain $[2, \infty)$ and codomain $[8, \infty)$. For surjectivity, the minimum value of $f(x)$ on $[2, \infty)$ must be $8$. The vertex of the parabola is at $x_v = \frac{p-2}{2}$.

Case 1: Vertex within the domain ($x_v \ge 2 \implies p \ge 6$). The minimum value is $f(x_v) = -\frac{(p-2)^2}{4} + 3p - 2$. Setting $f(x_v) = 8$: $-\frac{(p-2)^2}{4} + 3p - 2 = 8 \implies p^2 - 16p + 44 = 0$. The solutions are $p = \frac{16 \pm \sqrt{256 - 176}}{2} = \frac{16 \pm \sqrt{80}}{2} = \frac{16 \pm 4\sqrt{5}}{2} = 8 \pm 2\sqrt{5}$. Since $p \ge 6$, we check the values: $8 + 2\sqrt{5} > 6$ (valid). $8 - 2\sqrt{5} \approx 8 - 4.47 = 3.53 < 6$ (invalid). So, $p = 8 + 2\sqrt{5}$ is a valid value.

Case 2: Vertex to the left of the domain ($x_v < 2 \implies p < 6$). The function is increasing on $[2, \infty)$. The minimum value is $f(2)$. $f(2) = (2)^2 - (p-2)(2) + 3p - 2 = 4 - 2p + 4 + 3p - 2 = p+6$. Setting $f(2) = 8$: $p+6 = 8 \implies p=2$. Since $p < 6$, $p=2$ is a valid value.

The possible values of $p$ are $8 + 2\sqrt{5}$ and $2$. The sum of these values is $(8 + 2\sqrt{5}) + 2 = 10 + 2\sqrt{5}$. To match the form $m + \sqrt{n}$, we rewrite $2\sqrt{5} = \sqrt{4 \times 5} = \sqrt{20}$. So, the sum is $10 + \sqrt{20}$. Comparing with $m + \sqrt{n}$, we get $m=10$ and $n=20$. Both are natural numbers. The value to find is $\frac{n}{m} = \frac{20}{10} = 2$.