Question

If f : [2, ∞) → [8, ∞) is a surjective function defined by f (x) = x² - (p-2)x + 3p - 2, p ∈ R then sum of values of p is m + √n, where m, n ∈ N. Find the value of $\frac{n}{m}$.

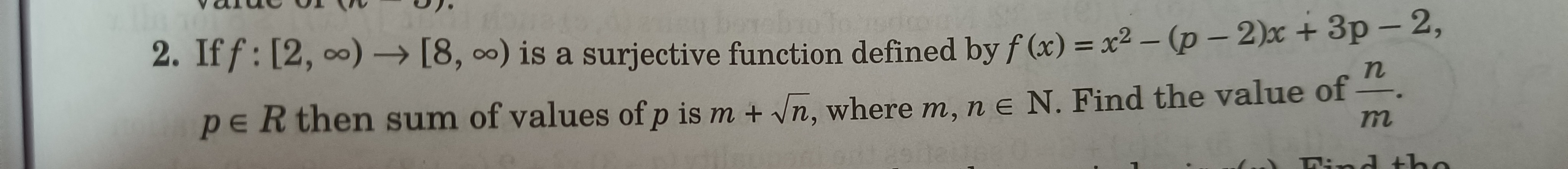
• A. The function is surjective, meaning its range on the given domain is equal to its codomain.
• B. The vertex of the parabola $y = x^2 - (p-2)x + 3p - 2$ is at $x_v = \frac{p-2}{2}$.
• C. Case 1: $x_v \ge 2$ (i.e., $p \ge 6$). The minimum value is $f(x_v) = -\frac{p^2}{4} + 4p - 3$. Setting this to 8 yields $p^2 - 16p + 44 = 0$, with solutions $p = 8 \pm 2\sqrt{5}$. Only $p = 8 + 2\sqrt{5}$ satisfies $p \ge 6$.
• D. Case 2: $x_v < 2$ (i.e., $p < 6$). The minimum value is $f(2) = p+6$. Setting this to 8 yields $p=2$, which satisfies $p < 6$.
• E. The sum of the valid values of p is $(8 + 2\sqrt{5}) + 2 = 10 + 2\sqrt{5} = 10 + \sqrt{20}$.
• F. Given the sum is $m + \sqrt{n}$, we have $m=10$ and $n=20$. Therefore, $\frac{n}{m} = \frac{20}{10} = 2$.

Answer 1

Answer: (F)

The sum of the valid values of p is $(8 + 2\sqrt{5}) + 2 = 10 + 2\sqrt{5} = 10 + \sqrt{20}$. Given the sum is $m + \sqrt{n}$, we have $m=10$ and $n=20$. Therefore, $\frac{n}{m} = \frac{20}{10} = 2$.

Answer 2

The problem requires finding values of $p$ such that the function $f(x) = x^2 - (p-2)x + 3p - 2$ is surjective from $[2, \infty)$ to $[8, \infty)$. This means the minimum value of $f(x)$ on the domain $[2, \infty)$ must be exactly 8.

The function is a parabola opening upwards. The vertex is at $x_v = \frac{p-2}{2}$.

Case 1: Vertex is in the domain ($x_v \ge 2$) This implies $\frac{p-2}{2} \ge 2$, so $p-2 \ge 4$, which means $p \ge 6$. In this case, the minimum value of $f(x)$ is at the vertex: $f(x_v) = \left(\frac{p-2}{2}\right)^2 - (p-2)\left(\frac{p-2}{2}\right) + 3p - 2$ $f(x_v) = -\frac{(p-2)^2}{4} + 3p - 2$ $f(x_v) = -\frac{p^2 - 4p + 4}{4} + 3p - 2$ $f(x_v) = -\frac{p^2}{4} + p - 1 + 3p - 2 = -\frac{p^2}{4} + 4p - 3$. Setting the minimum value to 8: $-\frac{p^2}{4} + 4p - 3 = 8$ $-\frac{p^2}{4} + 4p - 11 = 0$ Multiplying by -4: $p^2 - 16p + 44 = 0$. Using the quadratic formula: $p = \frac{16 \pm \sqrt{(-16)^2 - 4(1)(44)}}{2} = \frac{16 \pm \sqrt{256 - 176}}{2} = \frac{16 \pm \sqrt{80}}{2} = \frac{16 \pm 4\sqrt{5}}{2} = 8 \pm 2\sqrt{5}$. We must satisfy $p \ge 6$. $p_1 = 8 + 2\sqrt{5}$: Since $2\sqrt{5} > 0$, $p_1 > 8$, so $p_1 \ge 6$ is satisfied. $p_2 = 8 - 2\sqrt{5}$: Since $2\sqrt{5} = \sqrt{20}$ and $4 < \sqrt{20} < 5$, $8-5 < p_2 < 8-4$, so $3 < p_2 < 4$. This does not satisfy $p \ge 6$. So, $p = 8 + 2\sqrt{5}$ is a valid solution from this case.

Case 2: Vertex is to the left of the domain ($x_v < 2$) This implies $\frac{p-2}{2} < 2$, so $p-2 < 4$, which means $p < 6$. In this case, $f(x)$ is strictly increasing on $[2, \infty)$, and the minimum value occurs at $x=2$: $f(2) = (2)^2 - (p-2)(2) + 3p - 2$ $f(2) = 4 - 2p + 4 + 3p - 2 = p + 6$. Setting the minimum value to 8: $p + 6 = 8 \implies p = 2$. This satisfies the condition $p < 6$. So, $p=2$ is a valid solution.

The possible values for $p$ are $8 + 2\sqrt{5}$ and $2$. The sum of these values is $(8 + 2\sqrt{5}) + 2 = 10 + 2\sqrt{5}$. The problem states this sum is $m + \sqrt{n}$, where $m, n \in \mathbb{N}$. We rewrite $10 + 2\sqrt{5}$ as $10 + \sqrt{2^2 \times 5} = 10 + \sqrt{4 \times 5} = 10 + \sqrt{20}$. Comparing $10 + \sqrt{20}$ with $m + \sqrt{n}$, we have $m = 10$ and $n = 20$. Both are natural numbers. The value to find is $\frac{n}{m} = \frac{20}{10} = 2$.