Question
Question: If $\alpha, \beta$ are the roots of $x^2 - p(x+1) + c = 0$ then $(\alpha + 1)(\beta + 1) =$...
If α,β are the roots of x2−p(x+1)+c=0 then (α+1)(β+1)=
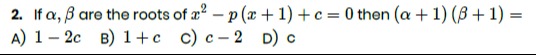
1-2c
1+c
c-2
c
1+c
Solution
The given equation is x2−p(x+1)+c=0. Expanding this, we get: x2−px−p+c=0
This is a quadratic equation of the form ax2+bx+d=0, where a=1, b=−p, and the constant term d=c−p. Let α and β be the roots of this equation. According to Vieta's formulas: The sum of the roots is α+β=−ab=−1−p=p. The product of the roots is αβ=ad=1c−p=c−p.
We need to find the value of (α+1)(β+1). Expanding this expression, we get: (α+1)(β+1)=αβ+α+β+1
Now, substitute the values of αβ and α+β obtained from Vieta's formulas: (α+1)(β+1)=(c−p)+(p)+1
Simplifying the expression: (α+1)(β+1)=c−p+p+1=c+1
Comparing this result with the given options: A) 1−2c B) 1+c C) c−2 D) c
The calculated value c+1 matches option B.
