Question

If $3\hat{j}$, $4\hat{k}$ and $3\hat{j}+4\hat{k}$ are position vectors of the vertices A, B, C respectively of $\triangle ABC$, then the position vector of the point in which the bisector of $\angle A$ meets BC is

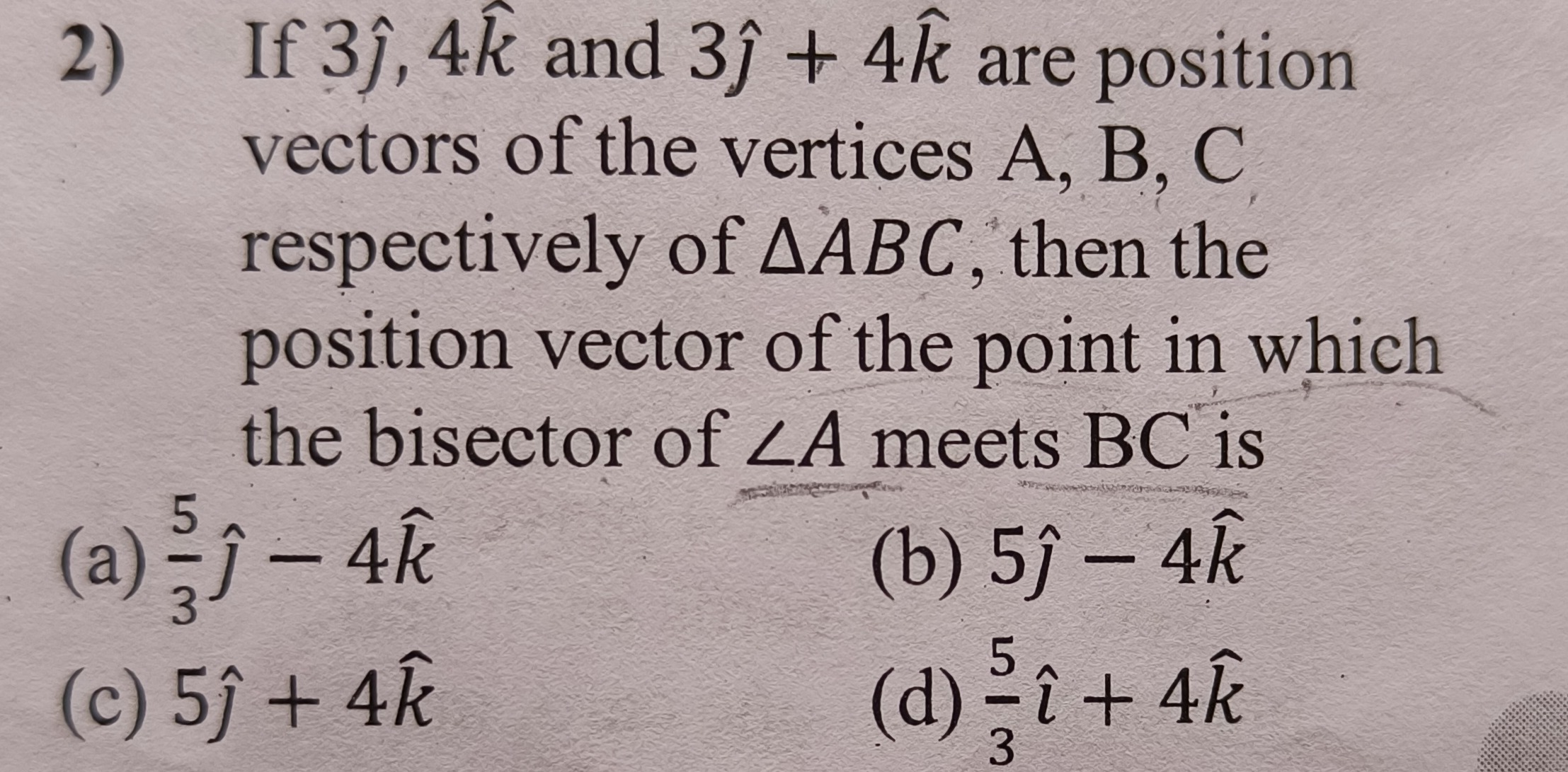
• A. $\frac{5}{3}\hat{j}-4\hat{k}$
• B. $5\hat{j}-4\hat{k}$
• C. $5\hat{j}+4\hat{k}$
• D. $\frac{5}{3}\hat{i}+4\hat{k}$

Answer 1

$\frac{5}{3}\hat{j}+4\hat{k}$

Answer 2

Let the vertices be

$$A=3\hat{j},\quad B=4\hat{k},\quad C=3\hat{j}+4\hat{k}.$$

In triangle ABC, the bisector of $\angle A$ meets side BC. By the Angle Bisector Theorem, if D is the point on BC where the bisector meets, then

$$\frac{BD}{DC}=\frac{AB}{AC}.$$

Step 1. Find lengths $AB$ and $AC$.

• $AB = |A-B| = |3\hat{j} - 4\hat{k}| = \sqrt{3^2 + 4^2} = 5.$
• $AC = |A-C| = |3\hat{j} - (3\hat{j}+4\hat{k})| = | - 4\hat{k}| = 4.$

Thus,

$$\frac{BD}{DC}=\frac{5}{4}.$$

Step 2. Write the position vectors of B and C:

$$B=4\hat{k},\quad C=3\hat{j}+4\hat{k}.$$

Using the section formula, the position vector of D (dividing BC in the ratio $BD:DC = 5:4$) is given by:

$$\vec{D}=\frac{4\,B + 5\,C}{5+4}=\frac{4(4\hat{k})+5(3\hat{j}+4\hat{k})}{9}.$$

Calculate:

$$4(4\hat{k})=16\hat{k},\quad 5(3\hat{j}+4\hat{k})=15\hat{j}+20\hat{k}.$$

Thus,

$$\vec{D}=\frac{15\hat{j}+(16+20)\hat{k}}{9}=\frac{15\hat{j}+36\hat{k}}{9}=\frac{5}{3}\hat{j}+4\hat{k}.$$

Therefore, the correct answer is $\frac{5}{3}\hat{j}+4\hat{k}$, which does not match any of the options exactly.