Question

2 identical balls are kept touching each other both have radius $R$. Find the relation between force of gravity and radius.

& A.\dfrac{1}{{{R}^{2}}} \\\ & B.\dfrac{1}{{{R}^{4}}} \\\ & C.{{R}^{4}} \\\ & D.{{R}^{3}} \\\ \end{aligned}$$

Answer 1

We have two identical balls which are in contact. Then the gravitational force between the centres of the two balls is given by the law of gravitation. From that equation we can find the relationship between the force and radius of the balls.

Formula used:
$F=G\dfrac{m_{1}m_{2}}{r^{2}}$

Complete step-by-step answer:
We know that the gravitational force is a non-contact force. We know that according to Newton-Kepler law of gravitation, gravitational force is given as, the force due to gravitation is given as $F=G\dfrac{m_{1}m_{2}}{r^{2}}$, where $G$ is the gravitational constant, $m_{1},m_{2}$ is the masses of the body, and $r$ is the distance between the two bodies.
Given that the two given balls are identical are in contact as shown in the figure below:

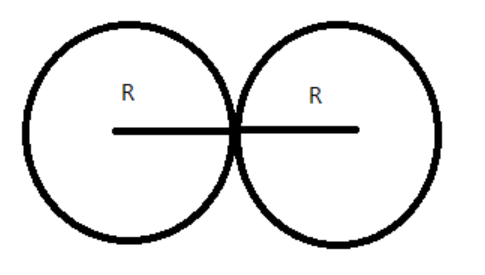
Since the balls are identical, we can say that the mass $m$ and the density $\rho$ of the balls are also equal.
Then we can also represent the mass of the identical balls as $m=\rho V=\dfrac{4}{3}R^{3}\rho$ where $V$ is the volume of the balls.
Then we can say that the gravitational force between the two balls is given as $F=\dfrac{Gm^{2}}{(2R)^{2}}=\dfrac{G\times \left(\dfrac{4}{3}R^{3}\rho\right)^{2}}{4R^{2}}=\dfrac{16GR^{6}\rho}{9\times 4R^{2}}$
$\implies F\propto\dfrac{R^{6}}{R^{2}}$
$\implies F\propto R^{4}$
Hence the answer is option $C.{{R}^{4}}$

So, the correct answer is “Option C”.

Note: Generally, gravitational force is given as $F=\dfrac{GMm}{r^{2}}$, where $G$ is the gravitational constant, $M$ and $m$ is the mass of the bigger and the smaller objects which are at a distance $r$ with respect to each other. Also note that, $m$ is the mass of the small object which is attracted
to a bigger object of mass $M$. Since the $M >> m$, we are considering on the effect of the small
body for finding the field. The acceleration due to gravitation on the surface of the earth is given as $g=\dfrac{Gm}{R^{2}}$ also, this value changes with respect to the height of the object from the centre of the earth. This force is generally attractive in nature.