Question
Question: 2. (ⅰ) $\frac{x-1}{x+1} \geq 0$ (ii) $\frac{x-2}{x+2} \geq 0$ (iii) $\frac{x-1}{x+1} \geq 1$ (iv) $\...
(ⅰ) x+1x−1≥0 (ii) x+2x−2≥0 (iii) x+1x−1≥1 (iv) x+5x−2>2 (v) 2x−3≤5, x+72x+5≥3 (vi) 7x−12x+1>5, x−8x+7>2 (vii) 35−2x≤6x−5 (viii) x−4x+7>2, x−22x+1>3 (ix) 21(53x+4)>31(x−6) (x) 52−3x<31−x<23+4x (xi) x+5>2(x+1), 2−x<3(x+2). (xii) 2(x−6)<3x−7, 11−2x<6−x. (xiii) −2−4x≤31+x, 3−x<4(x−3)
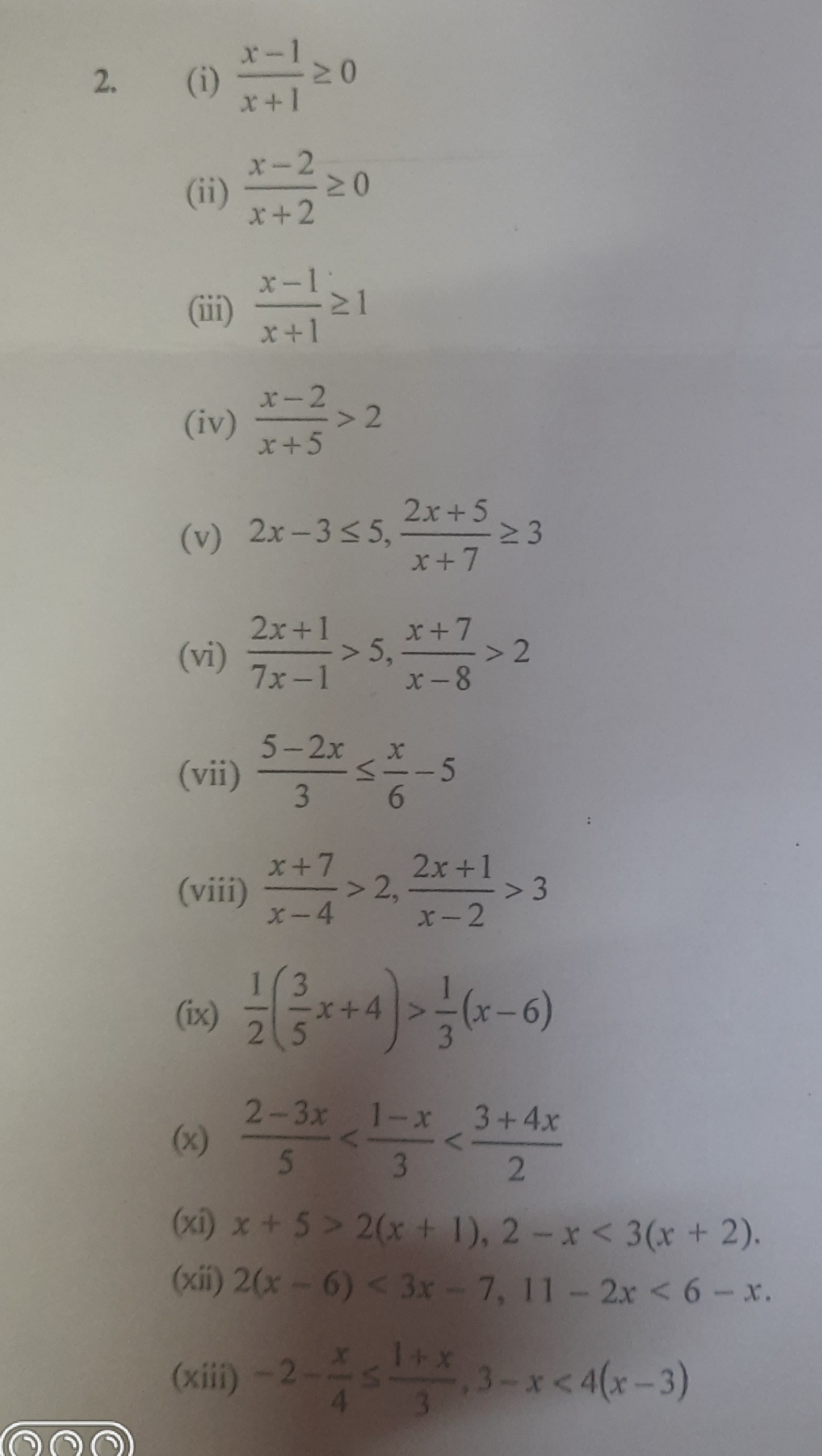
(i) x∈(−∞,−1)∪[1,∞) (ii) x∈(−∞,−2)∪[2,∞) (iii) x∈(−∞,−1) (iv) x∈(−12,−5) (v) x∈[−16,−7) (vi) No solution (∅) (vii) x∈[8,∞) (viii) x∈(4,7) (ix) x∈(−∞,120) (x) x∈(1/4,∞) (xi) x∈(−1,3) (xii) x∈(5,∞) (xiii) x∈(3,∞)
Solution
Here are the solutions for each inequality:
(i) x+1x−1≥0
Critical points are x=1 (from numerator) and x=−1 (from denominator). We test intervals:
- For x<−1 (e.g., x=−2): −2+1−2−1=−1−3=3≥0. (True)
- For −1<x<1 (e.g., x=0): 0+10−1=1−1=−1<0. (False)
- For x≥1 (e.g., x=2): 2+12−1=31≥0. (True)
Since the denominator cannot be zero, x=−1. Solution: x∈(−∞,−1)∪[1,∞)
(ii) x+2x−2≥0
Critical points are x=2 and x=−2. We test intervals:
- For x<−2 (e.g., x=−3): −3+2−3−2=−1−5=5≥0. (True)
- For −2<x<2 (e.g., x=0): 0+20−2=2−2=−1<0. (False)
- For x≥2 (e.g., x=3): 3+23−2=51≥0. (True)
Since x=−2. Solution: x∈(−∞,−2)∪[2,∞)
(iii) x+1x−1≥1
x+1x−1−1≥0 x+1x−1−(x+1)≥0 x+1−2≥0
For this inequality to hold, the denominator x+1 must be negative (since the numerator is negative and fixed at -2). x+1<0⟹x<−1. Solution: x∈(−∞,−1)
(iv) x+5x−2>2
x+5x−2−2>0 x+5x−2−2(x+5)>0 x+5x−2−2x−10>0 x+5−x−12>0
Multiply by -1 and reverse the inequality sign: x+5x+12<0
Critical points are x=−12 and x=−5. We test intervals:
- For x<−12 (e.g., x=−13): −13+5−13+12=−8−1=81<0. (False)
- For −12<x<−5 (e.g., x=−10): −10+5−10+12=−52=−52<0. (True)
- For x>−5 (e.g., x=0): 0+50+12=512<0. (False)
Solution: x∈(−12,−5)
(v) 2x−3≤5 and x+72x+5≥3
Inequality 1: 2x−3≤5 2x≤8⟹x≤4. Solution 1: (−∞,4]
Inequality 2: x+72x+5≥3 x+72x+5−3≥0 x+72x+5−3(x+7)≥0 x+72x+5−3x−21≥0 x+7−x−16≥0
Multiply by -1 and reverse the inequality sign: x+7x+16≤0
Critical points are x=−16 and x=−7. We test intervals:
- For x≤−16 (e.g., x=−20): −20+7−20+16=−13−4=134≤0. (False)
- For −16≤x<−7 (e.g., x=−10): −10+7−10+16=−36=−2≤0. (True)
- For x>−7 (e.g., x=0): 0+70+16=716≤0. (False)
Solution 2: [−16,−7)
Intersection of Solution 1 and Solution 2: (−∞,4]∩[−16,−7)=[−16,−7). Solution: x∈[−16,−7)
(vi) 7x−12x+1>5 and x−8x+7>2
Inequality 1: 7x−12x+1>5 7x−12x+1−5>0 7x−12x+1−5(7x−1)>0 7x−12x+1−35x+5>0 7x−1−33x+6>0
Multiply by -1/3 and reverse the inequality sign: 7x−111x−2<0
Critical points are x=2/11 and x=1/7. Since 1/7≈0.14 and 2/11≈0.18, 1/7<2/11. We test intervals:
- For x<1/7 (e.g., x=0): −1−2=2<0. (False)
- For 1/7<x<2/11 (e.g., x=0.15): 7(0.15)−111(0.15)−2=1.05−11.65−2=0.05−0.35=−7<0. (True)
- For x>2/11 (e.g., x=1): 7−111−2=69=1.5<0. (False)
Solution 1: (1/7,2/11)
Inequality 2: x−8x+7>2 x−8x+7−2>0 x−8x+7−2(x−8)>0 x−8x+7−2x+16>0 x−8−x+23>0
Multiply by -1 and reverse the inequality sign: x−8x−23<0
Critical points are x=23 and x=8. We test intervals:
- For x<8 (e.g., x=0): −8−23=823<0. (False)
- For 8<x<23 (e.g., x=10): 10−810−23=2−13=−6.5<0. (True)
- For x>23 (e.g., x=24): 24−824−23=161<0. (False)
Solution 2: (8,23)
Intersection of Solution 1 and Solution 2: (1/7,2/11)∩(8,23). Since 2/11≈0.18 and 8, there is no overlap. Solution: ∅ (No solution)
(vii) 35−2x≤6x−5
Multiply by the LCM of 3 and 6, which is 6: 6⋅35−2x≤6⋅(6x−5) 2(5−2x)≤x−30 10−4x≤x−30 10+30≤x+4x 40≤5x x≥540 x≥8 Solution: x∈[8,∞)
(viii) x−4x+7>2 and x−22x+1>3
Inequality 1: x−4x+7>2 x−4x+7−2>0 x−4x+7−2(x−4)>0 x−4x+7−2x+8>0 x−4−x+15>0
Multiply by -1 and reverse the inequality sign: x−4x−15<0
Critical points are x=15 and x=4. We test intervals:
- For x<4 (e.g., x=0): −4−15=415<0. (False)
- For 4<x<15 (e.g., x=5): 5−45−15=1−10=−10<0. (True)
- For x>15 (e.g., x=20): 20−420−15=165<0. (False)
Solution 1: (4,15)
Inequality 2: x−22x+1>3 x−22x+1−3>0 x−22x+1−3(x−2)>0 x−22x+1−3x+6>0 x−2−x+7>0
Multiply by -1 and reverse the inequality sign: x−2x−7<0
Critical points are x=7 and x=2. We test intervals:
- For x<2 (e.g., x=0): −2−7=27<0. (False)
- For 2<x<7 (e.g., x=3): 3−23−7=1−4=−4<0. (True)
- For x>7 (e.g., x=8): 8−28−7=61<0. (False)
Solution 2: (2,7)
Intersection of Solution 1 and Solution 2: (4,15)∩(2,7)=(4,7). Solution: x∈(4,7)
(ix) 21(53x+4)>31(x−6) 103x+2>31x−2 2+2>31x−103x 4>(3010−9)x 4>301x
Multiply by 30: 120>x Solution: x∈(−∞,120)
(x) 52−3x<31−x<23+4x
This is a system of two inequalities: Inequality 1: 52−3x<31−x Multiply by 15: 3(2−3x)<5(1−x) 6−9x<5−5x 6−5<−5x+9x 1<4x x>41 Solution 1: (1/4,∞)
Inequality 2: 31−x<23+4x Multiply by 6: 2(1−x)<3(3+4x) 2−2x<9+12x 2−9<12x+2x −7<14x x>14−7 x>−21 Solution 2: (−1/2,∞)
Intersection of Solution 1 and Solution 2: (1/4,∞)∩(−1/2,∞)=(1/4,∞). Solution: x∈(1/4,∞)
(xi) x+5>2(x+1) and 2−x<3(x+2)
Inequality 1: x+5>2(x+1) x+5>2x+2 5−2>2x−x 3>x Solution 1: (−∞,3)
Inequality 2: 2−x<3(x+2) 2−x<3x+6 2−6<3x+x −4<4x x>−1 Solution 2: (−1,∞)
Intersection of Solution 1 and Solution 2: (−∞,3)∩(−1,∞)=(−1,3). Solution: x∈(−1,3)
(xii) 2(x−6)<3x−7 and 11−2x<6−x
Inequality 1: 2(x−6)<3x−7 2x−12<3x−7 −12+7<3x−2x −5<x Solution 1: (−5,∞)
Inequality 2: 11−2x<6−x 11−6<−x+2x 5<x Solution 2: (5,∞)
Intersection of Solution 1 and Solution 2: (−5,∞)∩(5,∞)=(5,∞). Solution: x∈(5,∞)
(xiii) −2−4x≤31+x and 3−x<4(x−3)
Inequality 1: −2−4x≤31+x Multiply by 12: 12(−2)−12(4x)≤12(31+x) −24−3x≤4(1+x) −24−3x≤4+4x −24−4≤4x+3x −28≤7x x≥−4 Solution 1: [−4,∞)
Inequality 2: 3−x<4(x−3) 3−x<4x−12 3+12<4x+x 15<5x x>3 Solution 2: (3,∞)
Intersection of Solution 1 and Solution 2: [−4,∞)∩(3,∞)=(3,∞). Solution: x∈(3,∞)
Explanation of the solution:
Each problem involves solving one or more linear or rational inequalities.
- Linear Inequalities: Simplify by distributing, combining like terms, and isolating x. Remember to reverse the inequality sign if multiplying or dividing by a negative number.
- Rational Inequalities:
- Move all terms to one side to get Q(x)P(x)≥0 or Q(x)P(x)≤0.
- Find critical points by setting the numerator and denominator to zero.
- Plot critical points on a number line, dividing it into intervals.
- Test a value from each interval in the inequality to determine the sign.
- The solution is the union of intervals that satisfy the inequality. Remember that values making the denominator zero are excluded.
- Compound Inequalities (systems): Solve each inequality separately and then find the intersection of their solution sets.
Answer: (i) x∈(−∞,−1)∪[1,∞) (ii) x∈(−∞,−2)∪[2,∞) (iii) x∈(−∞,−1) (iv) x∈(−12,−5) (v) x∈[−16,−7) (vi) No solution (∅) (vii) x∈[8,∞) (viii) x∈(4,7) (ix) x∈(−∞,120) (x) x∈(1/4,∞) (xi) x∈(−1,3) (xii) x∈(5,∞) (xiii) x∈(3,∞)
