Question
Question: For x ∈ R, let [x] denote the greatest integer ≥ x, then the sum of the series $\left[-\frac{1}{3}\r...
For x ∈ R, let [x] denote the greatest integer ≥ x, then the sum of the series [−31]+[−31−1001]+........+[−31−10099] is:
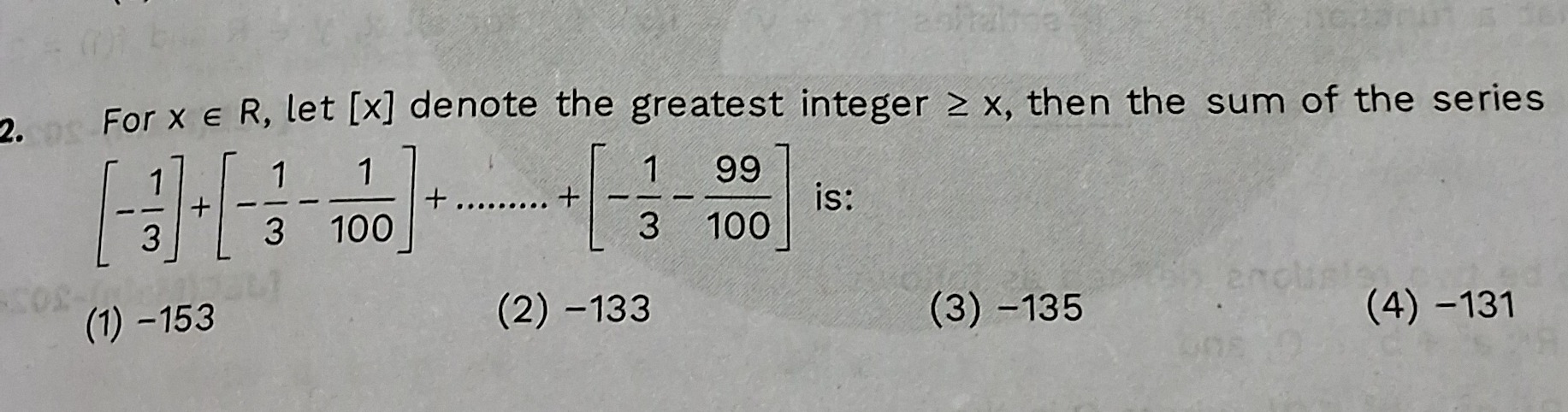
-153
-133
-135
-131
-133
Solution
The given series is S=[−31]+[−31−1001]+........+[−31−10099].
The general term of the series is ak=[−31−100k] for k=0,1,2,…,99. There are 100 terms in the series.
We need to evaluate the value of [−31−100k] for each k from 0 to 99. The value of [x] is the greatest integer less than or equal to x. Let's find the range of k for which the value of [−31−100k] is constant. We know that [x]=n if n≤x<n+1 for an integer n. So, [−31−100k]=n if n≤−31−100k<n+1. Multiplying by −1 and reversing the inequalities, we get −n−1<31+100k≤−n.
Let's find the values of n that the terms can take. For k=0, the term is [−31]=−1. So n=−1 occurs. For the term to be −1, we have −1≤−31−100k<0. 1≥31+100k>0. 32≥100k>−31. 3200≥k>−3100. 66.66…≥k>−33.33…. Since k starts from 0, the values of k for which [−31−100k]=−1 are k=0,1,…,66. The number of such terms is 66−0+1=67. The sum of these terms is 67×(−1)=−67.
Let's find when the value of the term is −2. So n=−2. For the term to be −2, we have −2≤−31−100k<−1. 2≥31+100k>1. 2−31≥100k>1−31. 35≥100k>32. 3500≥k>3200. 166.66…≥k>66.66…. The values of k in this range that are in our series (0≤k≤99) are k=67,68,…,99. The number of such terms is 99−67+1=33. The sum of these terms is 33×(−2)=−66.
Let's check if any term is −3. So n=−3. For the term to be −3, we have −3≤−31−100k<−2. 3≥31+100k>2. 3−31≥100k>2−31. 38≥100k>35. 3800≥k>3500. 266.66…≥k>166.66…. Since the maximum value of k in the series is 99, there are no terms with value −3 or less.
The total sum of the series is the sum of the terms with value −1 and the sum of the terms with value −2. Total sum S=(−67)+(−66)=−133.
