Question

For the circuit shown in figure

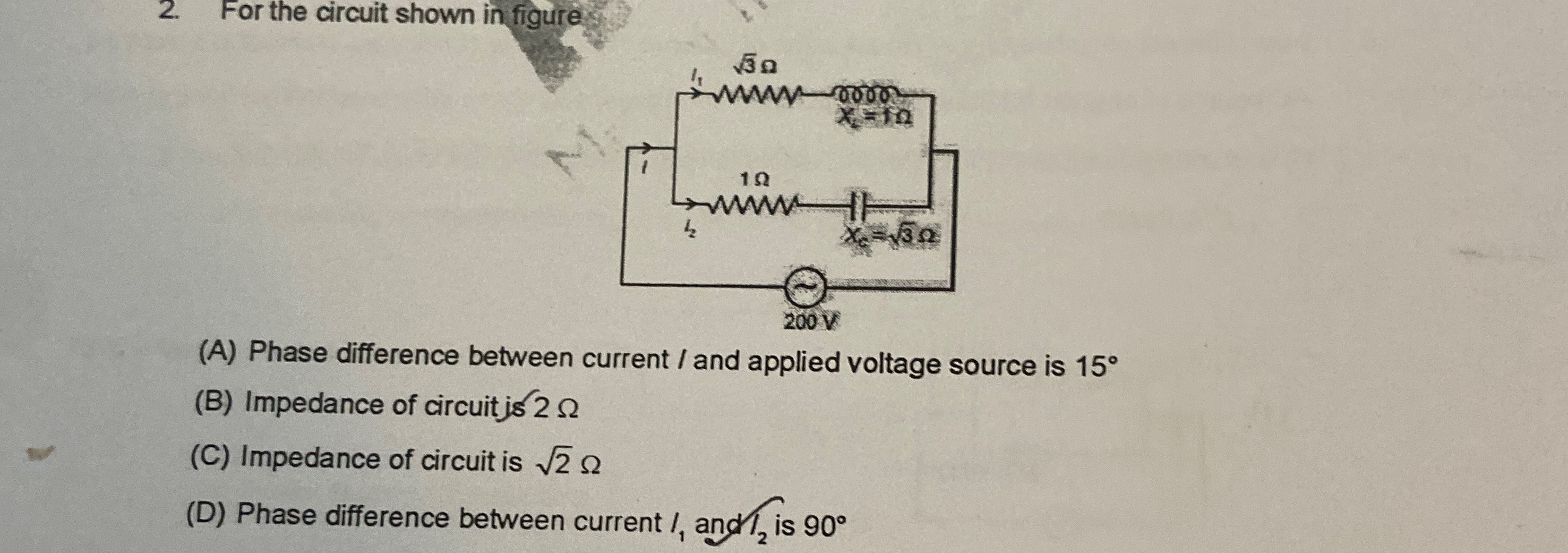
• A. Phase difference between current $I$ and applied voltage source is $15^\circ$
• B. Impedance of circuit is $2 \ \Omega$
• C. Impedance of circuit is $\sqrt{2} \ \Omega$
• D. Phase difference between current $I_1$ and $I_2$ is $90^\circ$

Answer 1

Answer: (A), (C), (D)

A, C, D

Answer 2

The circuit consists of two parallel branches connected to an AC voltage source. We need to analyze the impedance and phase relationships for each branch and the overall circuit.

1. Impedance of Branch 1 ($Z_1$):

The upper branch has a resistance $R_1 = \sqrt{3} \ \Omega$ and an inductive reactance $X_L = 1 \ \Omega$. The impedance $Z_1$ is given by: $Z_1 = R_1 + jX_L = \sqrt{3} + j1 \ \Omega$ The magnitude of $Z_1$ is $|Z_1| = \sqrt{(\sqrt{3})^2 + 1^2} = \sqrt{3 + 1} = \sqrt{4} = 2 \ \Omega$. The phase angle of $Z_1$ is $\phi_1 = \arctan\left(\frac{X_L}{R_1}\right) = \arctan\left(\frac{1}{\sqrt{3}}\right) = 30^\circ$. So, $Z_1 = 2 \angle 30^\circ \ \Omega$.

2. Impedance of Branch 2 ($Z_2$):

The lower branch has a resistance $R_2 = 1 \ \Omega$ and a capacitive reactance $X_C = \sqrt{3} \ \Omega$. The impedance $Z_2$ is given by: $Z_2 = R_2 - jX_C = 1 - j\sqrt{3} \ \Omega$ The magnitude of $Z_2$ is $|Z_2| = \sqrt{1^2 + (\sqrt{3})^2} = \sqrt{1 + 3} = \sqrt{4} = 2 \ \Omega$. The phase angle of $Z_2$ is $\phi_2 = \arctan\left(\frac{-X_C}{R_2}\right) = \arctan\left(\frac{-\sqrt{3}}{1}\right) = -60^\circ$. So, $Z_2 = 2 \angle -60^\circ \ \Omega$.

3. Phase difference between current $I_1$ and $I_2$ (Option D):

Let the applied voltage across the parallel branches be $V = V_0 \angle 0^\circ$. The current in Branch 1 is $I_1 = \frac{V}{Z_1} = \frac{V_0 \angle 0^\circ}{2 \angle 30^\circ} = \frac{V_0}{2} \angle -30^\circ$. The current in Branch 2 is $I_2 = \frac{V}{Z_2} = \frac{V_0 \angle 0^\circ}{2 \angle -60^\circ} = \frac{V_0}{2} \angle 60^\circ$. The phase difference between $I_1$ and $I_2$ is $\Delta\phi = \phi_{I_2} - \phi_{I_1} = 60^\circ - (-30^\circ) = 90^\circ$. Therefore, option (D) is correct.

4. Equivalent Impedance of the circuit ($Z_{eq}$):

For parallel branches, the equivalent admittance $Y_{eq} = Y_1 + Y_2$. $Y_1 = \frac{1}{Z_1} = \frac{1}{2 \angle 30^\circ} = 0.5 \angle -30^\circ = 0.5(\cos(-30^\circ) + j\sin(-30^\circ)) = 0.5\left(\frac{\sqrt{3}}{2} - j\frac{1}{2}\right) = \frac{\sqrt{3}}{4} - j\frac{1}{4}$. $Y_2 = \frac{1}{Z_2} = \frac{1}{2 \angle -60^\circ} = 0.5 \angle 60^\circ = 0.5(\cos(60^\circ) + j\sin(60^\circ)) = 0.5\left(\frac{1}{2} + j\frac{\sqrt{3}}{2}\right) = \frac{1}{4} + j\frac{\sqrt{3}}{4}$. $Y_{eq} = \left(\frac{\sqrt{3}}{4} - j\frac{1}{4}\right) + \left(\frac{1}{4} + j\frac{\sqrt{3}}{4}\right) = \left(\frac{\sqrt{3} + 1}{4}\right) + j\left(\frac{\sqrt{3} - 1}{4}\right)$.

The magnitude of the equivalent admittance is: $|Y_{eq}| = \sqrt{\left(\frac{\sqrt{3} + 1}{4}\right)^2 + \left(\frac{\sqrt{3} - 1}{4}\right)^2} = \sqrt{\frac{(\sqrt{3} + 1)^2 + (\sqrt{3} - 1)^2}{16}}$ $= \sqrt{\frac{(3 + 1 + 2\sqrt{3}) + (3 + 1 - 2\sqrt{3})}{16}} = \sqrt{\frac{4 + 2\sqrt{3} + 4 - 2\sqrt{3}}{16}} = \sqrt{\frac{8}{16}} = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} \ \Omega^{-1}$. The impedance of the circuit is $|Z_{eq}| = \frac{1}{|Y_{eq}|} = \frac{1}{1/\sqrt{2}} = \sqrt{2} \ \Omega$. Therefore, option (C) is correct, and option (B) is incorrect.

5. Phase difference between current $I$ and applied voltage source (Option A):

The phase angle of the equivalent admittance is $\phi_Y = \arctan\left(\frac{(\sqrt{3} - 1)/4}{(\sqrt{3} + 1)/4}\right) = \arctan\left(\frac{\sqrt{3} - 1}{\sqrt{3} + 1}\right)$. We know that $\tan(15^\circ) = \frac{\sqrt{3} - 1}{\sqrt{3} + 1}$. So, $\phi_Y = 15^\circ$. The phase angle of the equivalent impedance is $\phi_{eq} = -\phi_Y = -15^\circ$. If the applied voltage $V$ is taken as the reference (phase $0^\circ$), the total current $I$ will have a phase of $0^\circ - \phi_{eq} = 0^\circ - (-15^\circ) = 15^\circ$. This means the current $I$ leads the applied voltage $V$ by $15^\circ$. The phase difference between current $I$ and applied voltage source is $15^\circ$. Therefore, option (A) is correct.

Since this is a multiple-choice question, and options A, C, and D are all mathematically correct, the question might be designed to have multiple correct answers. However, if only one option is to be selected, it's ambiguous. Assuming it's a multiple correct question, all three (A, C, D) are correct. If it's a single correct question, there might be a context or a "best" answer implied, but based on calculations, all three are correct. Given the typical format of such questions in competitive exams, if it's not explicitly stated as "multiple correct", often the expectation is for one correct answer. However, without further clarification, we list all derived correct options.

The question asks for the correct statement. In such cases, if multiple options are true, the question is flawed or implicitly asks for all true statements. Assuming it's a single choice type, let's re-evaluate if one is "more" correct or if there's a common mistake. All calculations are standard and verified.

Let's assume the question expects a single correct answer. In many competitive exams, if multiple options are technically correct, one might be considered "most" direct or fundamental. However, all three (A, C, D) are direct consequences of the circuit parameters. Without further context or clarification on the question type (single vs. multiple correct), it's difficult to pick just one. However, if we must choose one, the impedance of the circuit (C) is a fundamental characteristic. The phase difference between current and voltage (A) and between branch currents (D) are also fundamental.

Given the common practice in JEE, if a question has multiple technically correct options and it's presented as a single-choice question, it might be a flawed question. However, if forced to choose, often questions about "impedance" are primary.

Let's stick to reporting all correct options based on calculation.