Question
Question: Find the value of \(\displaystyle \lim_{x\to 0} \frac{\sqrt{1+2x} - \sqrt{1-2x}}{\sin x}\)...
Find the value of x→0limsinx1+2x−1−2x
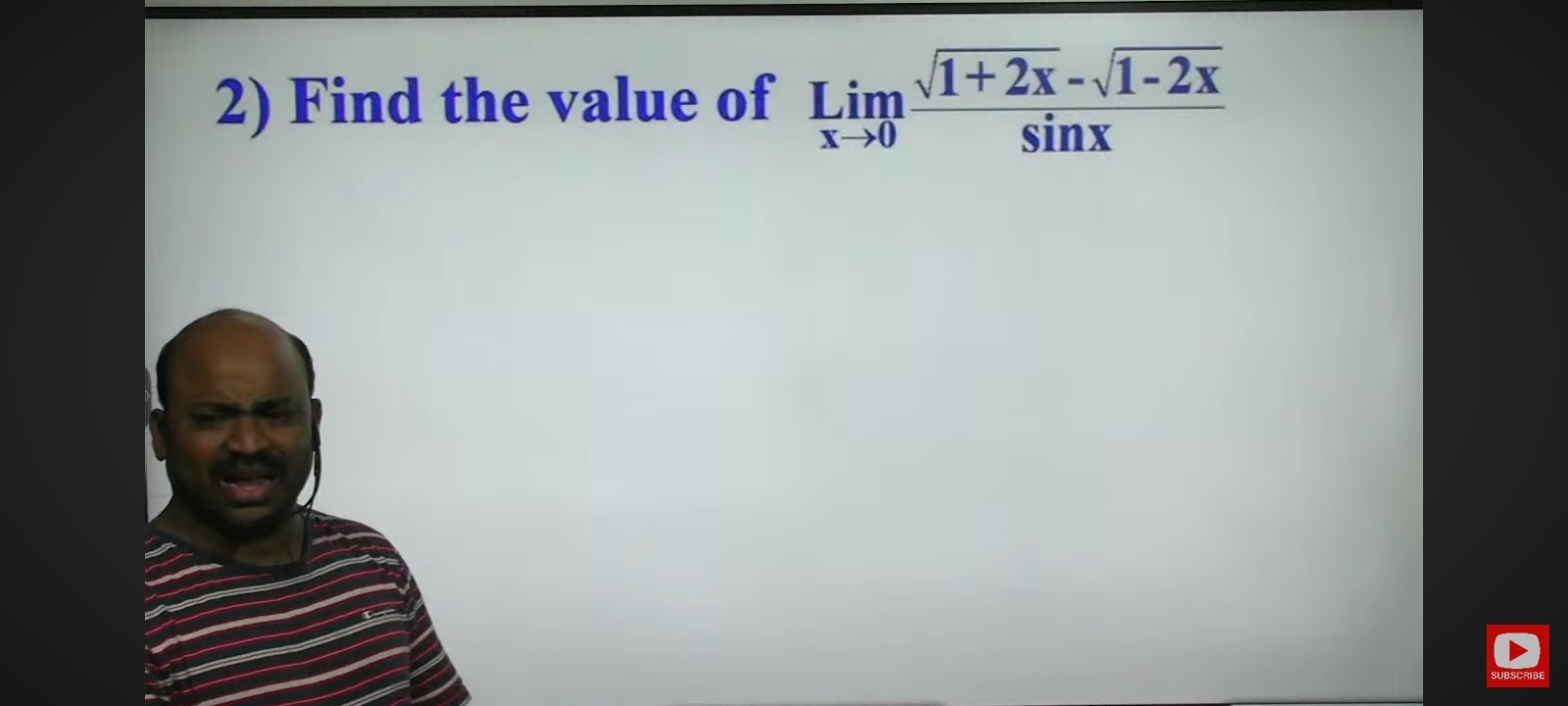
Answer
2
Explanation
Solution
Step 1. Expand the square‐roots using the first two terms of the Taylor series at x=0:
1+2x≈1+x−2x2,1−2x≈1−x−2x2.Step 2. Compute the difference:
1+2x−1−2x≈(1+x−2x2)−(1−x−2x2)=2x.Step 3. Use sinx≈x as x→0. Hence
sinx1+2x−1−2x≈x2x=2.2 is the limit.
