Question
Question: Find the point of intersection of tangents drawn at points (0,1) and (2,3) on $y=2x^2-3x+1$....
Find the point of intersection of tangents drawn at points (0,1) and (2,3) on y=2x2−3x+1.
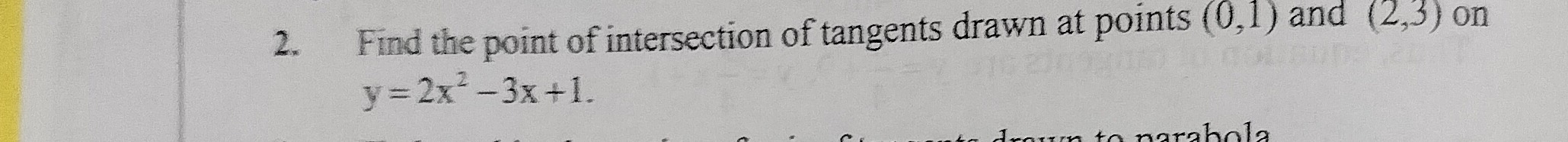
The point of intersection is (1, -2).
The point of intersection is (1, 2).
The point of intersection is (-1, -2).
The point of intersection is (-1, 2).
The point of intersection is (1, -2).
Solution
-
Find the derivative of the curve: The given curve is y=2x2−3x+1. The derivative is dxdy=4x−3.
-
Find the equation of the tangent at (0,1): The slope of the tangent at x=0 is m1=4(0)−3=−3. Using the point-slope form y−y1=m(x−x1): y−1=−3(x−0) y=−3x+1 (Equation 1)
-
Find the equation of the tangent at (2,3): The slope of the tangent at x=2 is m2=4(2)−3=8−3=5. Using the point-slope form y−y1=m(x−x1): y−3=5(x−2) y−3=5x−10 y=5x−7 (Equation 2)
-
Find the point of intersection: Equate Equation 1 and Equation 2: −3x+1=5x−7 8x=8 x=1 Substitute x=1 into Equation 1: y=−3(1)+1=−2. The point of intersection is (1, -2).
