Question
Question: Find the condition that line $lx+my+n=0$ touches the parabola $x^2=4ay$....
Find the condition that line lx+my+n=0 touches the parabola x2=4ay.
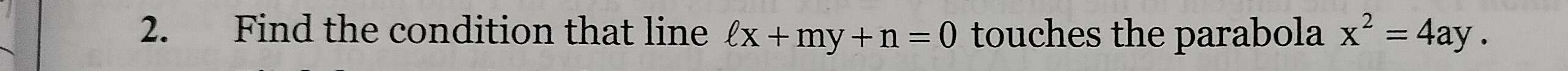
mn = al^2
ml = an^2
nl = am^2
ln = am^2
mn = al^2
Solution
To find the condition for the line lx+my+n=0 to touch the parabola x2=4ay, we can substitute the expression for y from the line equation into the parabola equation.
Assuming m=0, we can write y from the line equation as: my=−lx−n y=−mlx−mn
Substitute this into the parabola equation x2=4ay: x2=4a(−mlx−mn)
Multiply by m to clear the denominator: mx2=−4alx−4an
Rearrange this into a quadratic equation in x: mx2+4alx+4an=0
For the line to be tangent to the parabola, this quadratic equation must have exactly one real solution for x. This occurs when the discriminant (Δ) of the quadratic equation is zero. The discriminant of Ax2+Bx+C=0 is Δ=B2−4AC.
In this case, A=m, B=4al, and C=4an. Δ=(4al)2−4(m)(4an)=0 16a2l2−16amn=0
Assuming a=0 (for it to be a parabola), we can divide by 16a: al2−mn=0 mn=al2
This is the condition for tangency when m=0.
If m=0, the line equation becomes lx+n=0. For this to represent a line, l=0. The equation simplifies to x=−ln, which is a vertical line. Substituting this into the parabola equation x2=4ay: (−ln)2=4ay l2n2=4ay y=4al2n2 This gives a unique value for y, meaning the vertical line intersects the parabola at exactly one point, so it is tangent.
The condition mn=al2 derived for m=0 is the standard condition for the line lx+my+n=0 to touch the parabola x2=4ay. Although the derivation explicitly assumed m=0, the condition mn=al2 is generally accepted as the condition for tangency, covering all cases. The case m=0 leads to 0=al2, which implies l=0 if a=0. This appears contradictory as m=0 requires l=0 for a line. However, the condition mn=al2 is the established result.
