Question

Find the condition for the line $x \cos \theta + y \sin \theta = P$ to be a tangent to the ellipse $5x^2 + 7y^2 = 112$?

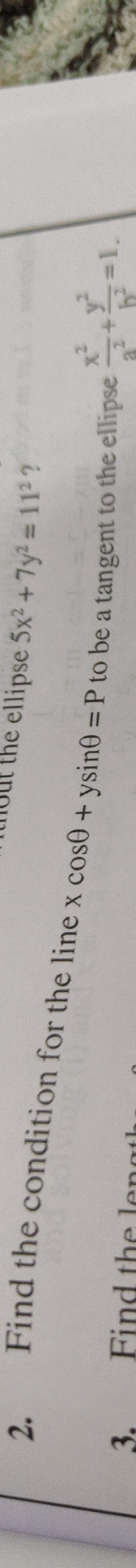
Answer 1

The condition is $P^2 = \frac{112}{5} \cos^2 \theta + 16 \sin^2 \theta$.

Answer 2

The standard form of the ellipse is $\frac{x^2}{112/5} + \frac{y^2}{16} = 1$, so $a^2 = \frac{112}{5}$ and $b^2 = 16$. The condition for the line $x \cos \theta + y \sin \theta = P$ to be tangent to the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ is $P^2 = a^2 \cos^2 \theta + b^2 \sin^2 \theta$. Substituting the values of $a^2$ and $b^2$ gives $P^2 = \frac{112}{5} \cos^2 \theta + 16 \sin^2 \theta$.