Solveeit Logo
Login

Question

Question: Examine the consistency and solve if consistent. 2x + 3y + 5z = 1 3x + y - z = 2 x + 4y - 6z = 1...

Examine the consistency and solve if consistent. 2x + 3y + 5z = 1 3x + y - z = 2 x + 4y - 6z = 1

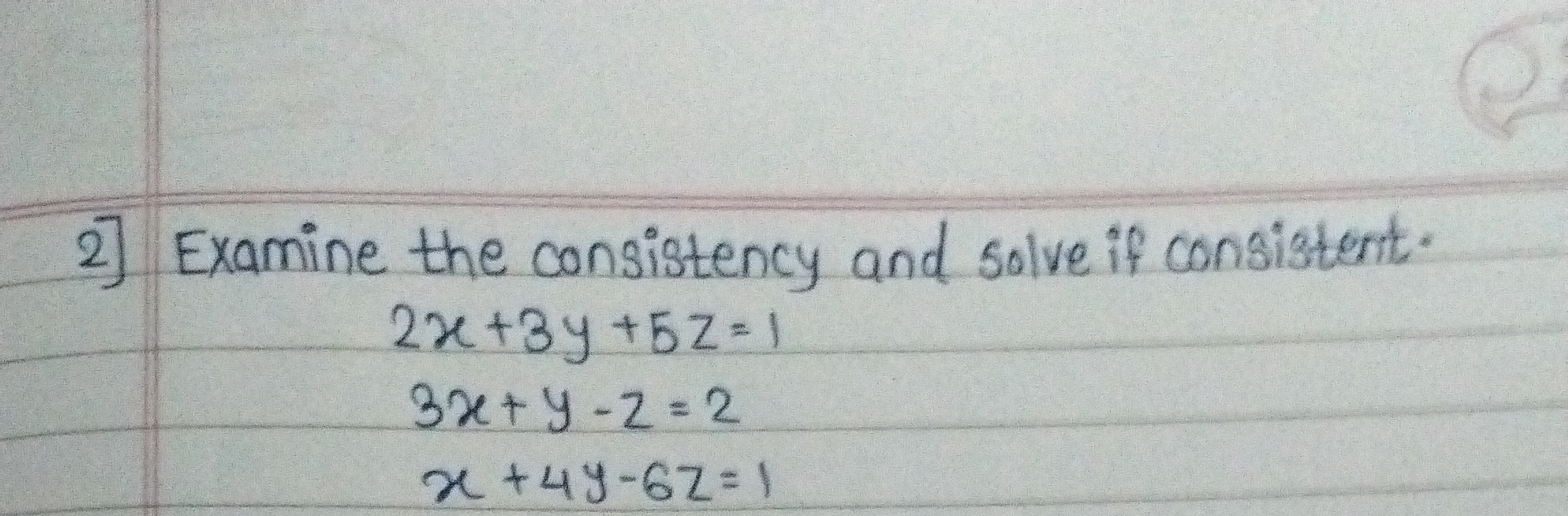
Answer

The system is consistent and has a unique solution. The solution is: x=1117,y=0,z=−117x = \frac{11}{17}, y = 0, z = -\frac{1}{17}

Explanation

Solution

The system of linear equations is represented by the augmented matrix [A∣B][A|B]. Row reduction to echelon form is performed to determine the ranks of the coefficient matrix AA and the augmented matrix [A∣B][A|B].

[A∣B]=(235∣131−1∣214−6∣1)[A|B] = \begin{pmatrix} 2 & 3 & 5 & | & 1 \\ 3 & 1 & -1 & | & 2 \\ 1 & 4 & -6 & | & 1 \end{pmatrix}

Applying row operations:

→R1↔R3(14−6∣131−1∣2235∣1)→R2←R2−3R1,R3←R3−2R1(14−6∣10−1117∣−10−517∣−1)→R3←R3−511R2(14−6∣10−1117∣−100102/11∣−6/11)\xrightarrow{R1 \leftrightarrow R3} \begin{pmatrix} 1 & 4 & -6 & | & 1 \\ 3 & 1 & -1 & | & 2 \\ 2 & 3 & 5 & | & 1 \end{pmatrix} \xrightarrow{R2 \leftarrow R2-3R1, R3 \leftarrow R3-2R1} \begin{pmatrix} 1 & 4 & -6 & | & 1 \\ 0 & -11 & 17 & | & -1 \\ 0 & -5 & 17 & | & -1 \end{pmatrix} \xrightarrow{R3 \leftarrow R3 - \frac{5}{11}R2} \begin{pmatrix} 1 & 4 & -6 & | & 1 \\ 0 & -11 & 17 & | & -1 \\ 0 & 0 & 102/11 & | & -6/11 \end{pmatrix}

The rank of the coefficient matrix AA is 3, and the rank of the augmented matrix [A∣B][A|B] is also 3. Since rank(A)=rank([A∣B])=3rank(A) = rank([A|B]) = 3, which is equal to the number of variables, the system is consistent and has a unique solution. Back-substitution yields the solution.