Question

Evaluate the integral $\int_{1}^{4}\int_{0}^{\sqrt{x}}\frac{3}{2}e^{y/\sqrt{x}}dydx.$

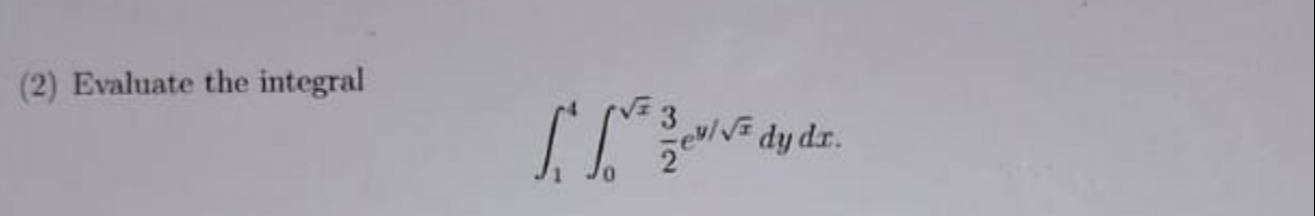
Answer 1

7(e-1)

Answer 2

Evaluate the inner integral $\int_{0}^{\sqrt{x}}\frac{3}{2}e^{y/\sqrt{x}}dy$ using substitution $u=y/\sqrt{x}$, yielding $\frac{3\sqrt{x}}{2}(e-1)$. Then, evaluate the outer integral $\int_{1}^{4} \frac{3\sqrt{x}}{2}(e-1) dx$. This simplifies to $\frac{3(e-1)}{2}\int_{1}^{4} x^{1/2} dx$. Applying the power rule and limits gives $(e-1)[x^{3/2}]_{1}^{4}$, which evaluates to $(e-1)(8-1) = 7(e-1)$.