Solveeit Logo
Login

Question

Question: \[2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\] is valid for all the values o...

2cos⁡−1x=sin⁡−1(2x1−x2)2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right) is valid for all the values of x satisfying
(a) −1≤x≤1-1\le x\le 1
(b) 0≤x≤10\le x\le 1
(c) 12≤x≤1\dfrac{1}{\sqrt{2}}\le x\le 1
(d) 0≤x≤120\le x\le \dfrac{1}{\sqrt{2}}

Explanation

Solution

Hint: We know that the range of sin⁡−12x1−x2{{\sin }^{-1}}2x\sqrt{1-{{x}^{2}}} is [−π2,π2]\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right], so the same would be for 2cos⁡−1x2{{\cos }^{-1}}x. From this, find the range of cos⁡−1x{{\cos }^{-1}}x and then find the value of x for which it is true.

Complete step-by-step answer:
We are given an equation 2cos⁡−1x=sin⁡−1(2x1−x2)2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right). We have to solve it and find all the values of x that satisfy this.
Let us consider the equation i.e. : 2cos⁡−1x=sin⁡−1(2x1−x2)2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)
We know that the range of sin⁡−1t{{\sin }^{-1}}t is [−π2,π2]\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right].
So, we also get the range sin⁡−1(2x1−x2){{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right) as [−π2,π2]\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]
Or, −π2≤sin⁡−1(2x1−x2)≤π2\dfrac{-\pi }{2}\le {{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right)\le \dfrac{\pi }{2}
Since, we know that 2cos⁡−1x=sin⁡−1(2x1−x2)2{{\cos }^{-1}}x={{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right) then, 2cos⁡−1x2{{\cos }^{-1}}x will also have the same range as sin⁡−1(2x1−x2){{\sin }^{-1}}\left( 2x\sqrt{1-{{x}^{2}}} \right). So, we get,
−π2≤2cos⁡−1x≤π2\dfrac{-\pi }{2}\le 2{{\cos }^{-1}}x\le \dfrac{\pi }{2}
By dividing 2 in the above equation, we get,
−π22≤2cos⁡−1x2≤π22\dfrac{\dfrac{-\pi }{2}}{2}\le \dfrac{2{{\cos }^{-1}}x}{2}\le \dfrac{\dfrac{\pi }{2}}{2}
Or, −π4≤cos⁡−1x≤π4\dfrac{-\pi }{4}\le {{\cos }^{-1}}x\le \dfrac{\pi }{4}
Now, we will draw the graph of cos⁡−1x{{\cos }^{-1}}x to analyze the above inequality.

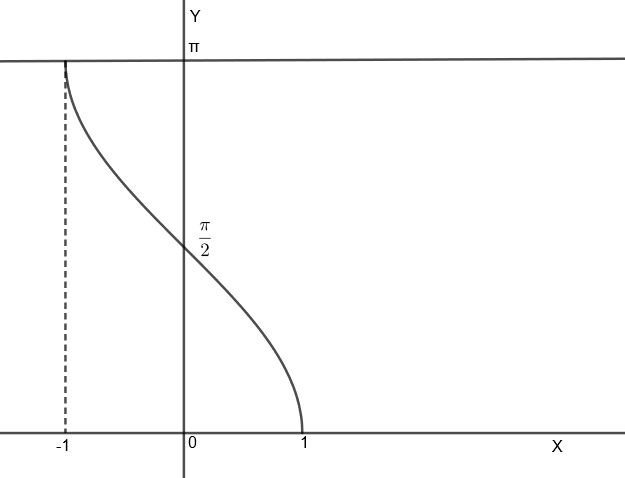
Since, we can see that the range of cos⁡−1x{{\cos }^{-1}}x is [0,π]\left[ 0,\pi \right], so we will get the range of cos⁡−1x{{\cos }^{-1}}x in this question as, 0≤cos⁡−1x≤π40\le {{\cos }^{-1}}x\le \dfrac{\pi }{4} because cos⁡−1x{{\cos }^{-1}}x cannot take negative values.
For cos⁡−1x=0{{\cos }^{-1}}x=0, we get x = cos 0 = 1.
And for cos⁡−1x=π4{{\cos }^{-1}}x=\dfrac{\pi }{4}, we get x=cos⁡π4=12x=\cos \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}.
So, we get, 12≤x≤1\dfrac{1}{\sqrt{2}}\le x\le 1.
Hence, option (c) is the right answer.

Note: In this question, we can also consider the graph of cos⁡−1x{{\cos }^{-1}}x to solve the inequality
0≤cos⁡−1x≤π40\le {{\cos }^{-1}}x\le \dfrac{\pi }{4}

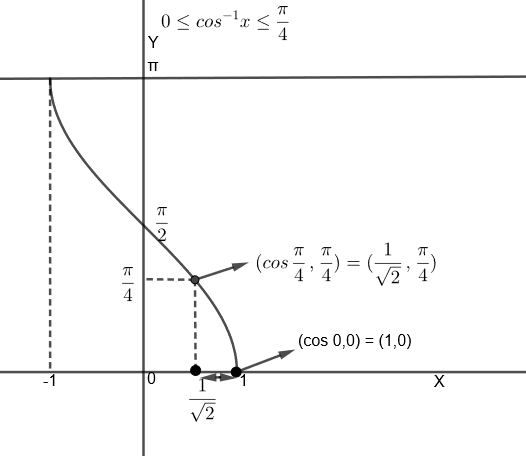
From the above graph, we can see that, when cos⁡−1x∈[0,π4]{{\cos }^{-1}}x\in \left[ 0,\dfrac{\pi }{4} \right], then x∈[12,1]x\in \left[ \dfrac{1}{\sqrt{2}},1 \right]. In questions involving the inverse trigonometric functions, take the special case of range and domain of the function.