Question
Question: Consider a large drop of liquid on a glass plate. Contact angle is $\theta$ and density of liquid is...
Consider a large drop of liquid on a glass plate. Contact angle is θ and density of liquid is ρ. Surface tension is S
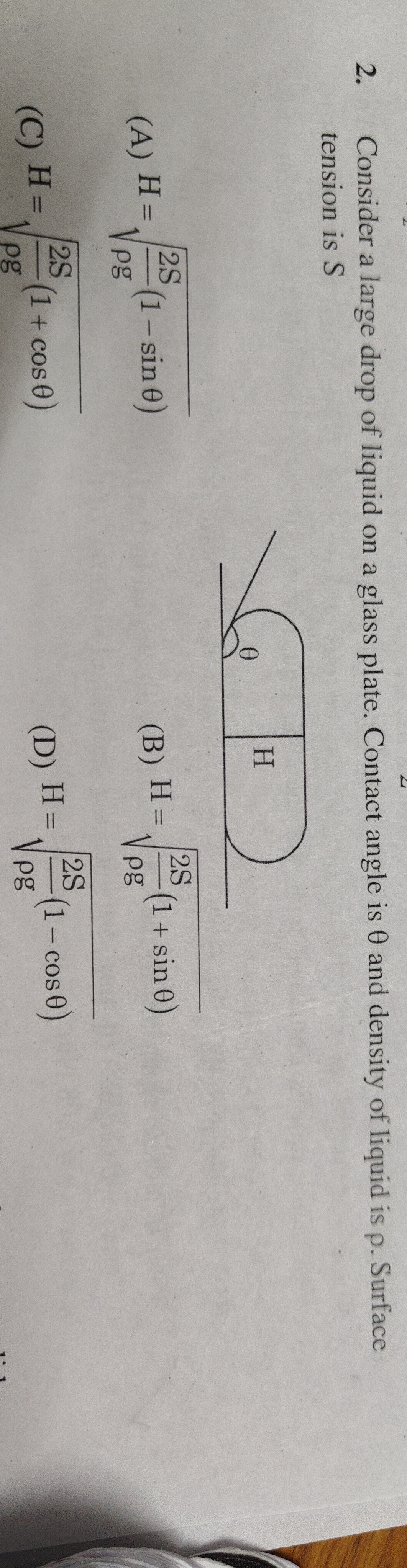
H = ρg2S(1−sinθ)
H = ρg2S(1+sinθ)
H = ρg2S(1+cosθ)
H = ρg2S(1−cosθ)
H = ρg2S(1−sinθ)
Solution
For a sessile drop (a drop resting on a surface), the height H is related to surface tension S, density ρ, and contact angle θ. Assuming the drop is a spherical cap and balancing the hydrostatic pressure (ρgH) with the capillary pressure (R2S), where R is the radius of curvature, we have ρgH=R2S. The relationship between the height H and the radius of curvature R for a spherical cap is H=R(1−sinθ). Substituting R from this equation into the pressure balance gives ρgH=1−sinθH2S. Rearranging this equation yields H2=ρg2S(1−sinθ), and thus H=ρg2S(1−sinθ).
