Question
Question: 0.30 g of a volatile liquid displaces 90.0 $cm^3$ of air at STP in the Victor Meyer's method. The mo...
0.30 g of a volatile liquid displaces 90.0 cm3 of air at STP in the Victor Meyer's method. The molecular mass of the liquid is:
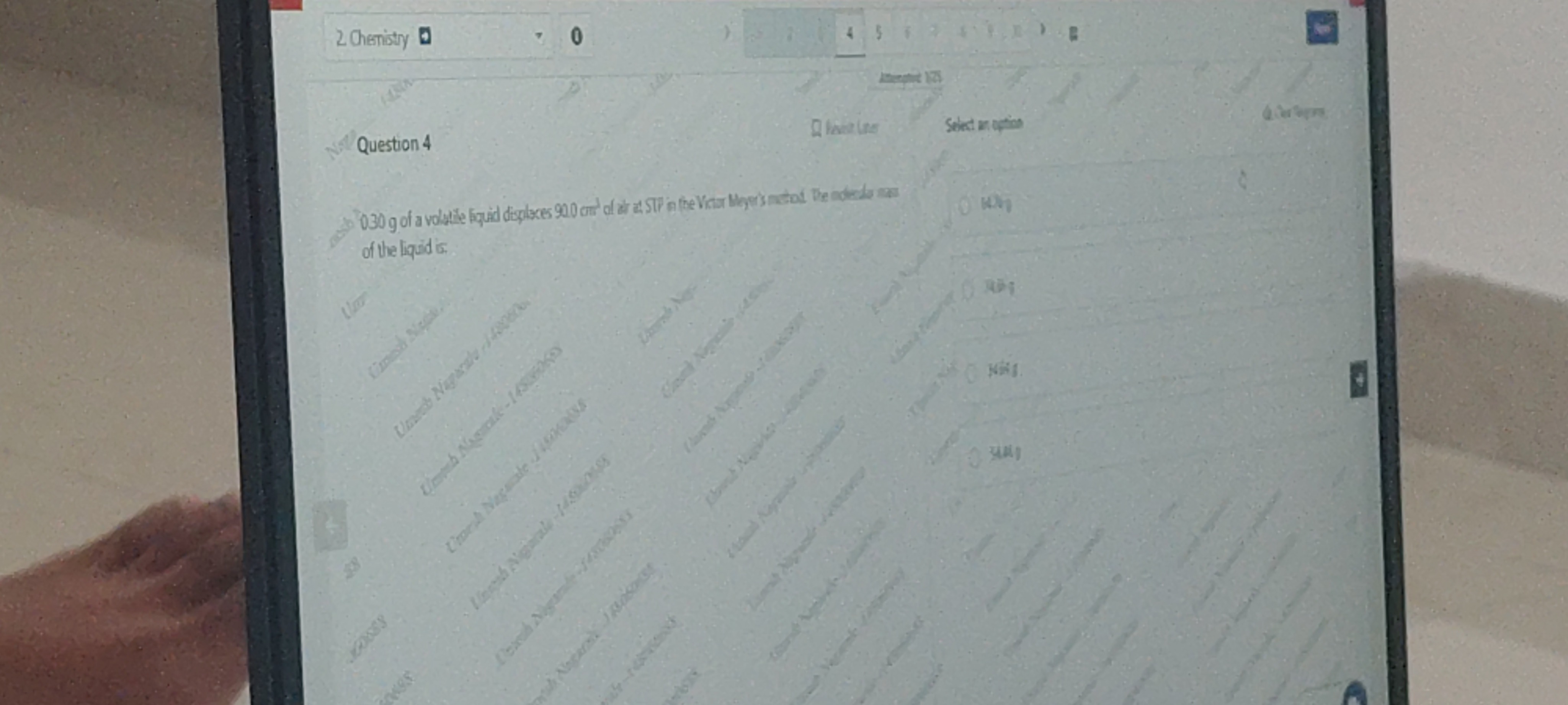
64.7g
74.8 g
349.4 g
54.8 g
74.8 g
Solution
The Victor Meyer's method is used to determine the molecular mass of a volatile substance by measuring the volume of its vapor. In this method, the volume of air displaced by the vapor of the substance at a given temperature and pressure is measured. This displaced volume is equal to the volume occupied by the vapor of the substance under the same conditions.
Given: Mass of the volatile liquid (m) = 0.30 g Volume of air displaced at STP (V) = 90.0 cm³
At STP (Standard Temperature and Pressure), the molar volume of any ideal gas is 22.4 L/mol or 22400 cm³/mol. This means that 1 mole of any gas occupies 22400 cm³ at STP.
The volume of air displaced is 90.0 cm³ at STP, which means the volume of the vapor of the liquid is also 90.0 cm³ at STP.
We can find the number of moles (n) of the vapor using the molar volume at STP: n=Molar volume at STPVolume of vapor n=22400 cm3/mol90.0 cm3
Now, we can calculate the molecular mass (M) of the liquid using the formula: M=Number of moles (n)Mass of liquid (m) Substitute the values of m and n: M=2240090.0 mol0.30 g M=90.0 cm30.30 g×22400 cm3/mol M=90.06720 g/mol M=74.666... g/mol
Rounding the result to an appropriate number of significant figures (considering 0.30 g has two significant figures and 90.0 cm³ has three), we can round it to one decimal place, which gives 74.7 g/mol.
Comparing this value with the given options, the calculated value of 74.666... g/mol is closest to 74.8 g.
