Question

Area of the triangle formed by the lines with equal intercepts on the axes & which touch the ellipse $\frac{x^2}{16}+\frac{y^2}{9}=1$ and positive coordinate axes is $\frac{100A+B}{2}$ (Where A & B $\epsilon$ positive integers), then value of 'B - 10A' is equal to

Answer 1

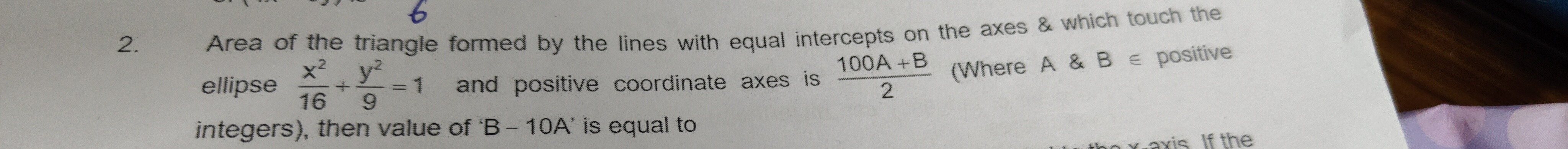
25

Answer 2

The ellipse is $\frac{x^2}{16}+\frac{y^2}{9}=1$, so $a^2=16, b^2=9$. A line with equal intercepts on the axes has the form $x+y=k$ or $x-y=k$. For the line to touch the ellipse, the condition is $a^2m^2+b^2=c^2$ for $y=mx+c$ or $a^2A^2+b^2B^2=C^2$ for $Ax+By+C=0$. Consider $x+y=k$. Here $m=-1, c=k$. The condition is $16(-1)^2 + 9 \ne k^2$ (this is for $y=mx+c$ form, not $x+y=k$). The condition for $Ax+By+C=0$ to touch $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is $a^2A^2+b^2B^2=C^2$. For $x+y-k=0$, $A=1, B=1, C=-k$. So $16(1)^2+9(1)^2=(-k)^2 \implies 25 = k^2 \implies k = \pm 5$. The lines are $x+y=5$ and $x+y=-5$. For $x-y=k$, $A=1, B=-1, C=-k$. So $16(1)^2+9(-1)^2=(-k)^2 \implies 25 = k^2 \implies k = \pm 5$. The lines are $x-y=5$ and $x-y=-5$.

The problem states "positive coordinate axes". This implies the intercepts must be positive. For $x+y=5$, x-intercept ($y=0$) is $x=5$, y-intercept ($x=0$) is $y=5$. Both are positive. For $x+y=-5$, intercepts are -5 and -5. For $x-y=5$, x-intercept is 5, y-intercept is -5. For $x-y=-5$, x-intercept is -5, y-intercept is 5.

The only line forming a triangle with positive coordinate axes is $x+y=5$. The intercepts are 5 and 5. The area of this triangle is $\frac{1}{2} \times 5 \times 5 = \frac{25}{2}$.

We are given the area is $\frac{100A+B}{2}$. So, $25 = 100A+B$. Since A and B are positive integers, this equation has no solution. If $A \ge 1$, $100A \ge 100$, making $B$ negative. Assuming A is a non-negative integer and B is a positive integer, we have $A=0$ and $B=25$. Then, $B-10A = 25 - 10(0) = 25$.